题目内容
设数列{an}的前n项和为Sn,a1=1,(cosα+sinα)an+1=sinα•Sn+2cosα-sinα,(n∈N*),α∈(0,π),若对任意n∈N*,an+1>an>0恒成立,则α的取值范围为 .
考点:数列递推式
专题:等差数列与等比数列
分析:当n≥2时,an=Sn-Sn-1,再利用对任意n∈N*,an+1>an>0恒成立,三角函数的单调性即可得出.
解答:
解:当n≥2时,(cosα+sinα)an+1=sinα•Sn+2cosα-sinα,
(cosα+sinα)an=sinα•Sn-1+2cosα-sinα,
∴(cosα+sinα)an+1-(cosα+sinα)an=sinα•an.
∴(cosα+sinα)an+1=(cosα+2sinα)an.
又对任意n∈N*,an+1>an>0恒成立,
∴
=
>1.
∴
>0.
∵α∈(0,π),
∴sinα>0.
∴cosα+sinα>0,
∴α∈(0,
).
故答案为:(0,
).
(cosα+sinα)an=sinα•Sn-1+2cosα-sinα,
∴(cosα+sinα)an+1-(cosα+sinα)an=sinα•an.
∴(cosα+sinα)an+1=(cosα+2sinα)an.
又对任意n∈N*,an+1>an>0恒成立,
∴
| an+1 |
| an |
| cosα+2sinα |
| cosα+sinα |
∴
| sinα |
| cosα+sinα |
∵α∈(0,π),
∴sinα>0.
∴cosα+sinα>0,
∴α∈(0,
| 3π |
| 4 |
故答案为:(0,
| 3π |
| 4 |
点评:本题考查了利用“当n≥2时,an=Sn-Sn-1”、数列的单调性、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
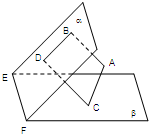 如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影
如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影 如图是定义在区间[-2,2]的函数y=f(x),则f(x)的减区间是
如图是定义在区间[-2,2]的函数y=f(x),则f(x)的减区间是