题目内容
已知函数f（x）=
-
，（a∈R且a＞0）．
（1）判断函数f（x）的单调性，并证明；
（2）若函数f（x）的定义域为（-2，2）时，求使f（1-m）-f（m2-1）＜0成立的实数m的取值范围．
| ex |
| a |
| a |
| ex |
（1）判断函数f（x）的单调性，并证明；
（2）若函数f（x）的定义域为（-2，2）时，求使f（1-m）-f（m2-1）＜0成立的实数m的取值范围．
考点：函数单调性的判断与证明,函数单调性的性质
专题：函数的性质及应用,导数的综合应用
分析：（1）求f′（x），根据f′（x）的符号即可判断函数f（x）的单调性；
（2）由f（1-m）-f（m2-1）＜0得，f（1-m）＜f（m2-1），根据f（x）在（-2，2）上的单调性及定义域（-2，2）即可得到关于m的不等式组，解不等式组即得m的取值范围．
（2）由f（1-m）-f（m2-1）＜0得，f（1-m）＜f（m2-1），根据f（x）在（-2，2）上的单调性及定义域（-2，2）即可得到关于m的不等式组，解不等式组即得m的取值范围．
解答：
解：（1）f′（x）=
+
；
∵a＞0，∴f′（x）＞0；
∴f（x）在R上是增函数；
（2）由原不等式得：f（1-m）＜f（m2-1）；
∵f（x）在（-2，2）上是增函数，所以：
，解得1＜m＜
；
∴实数m的取值范围是(1，
)．
| ex |
| a |
| a |
| ex |
∵a＞0，∴f′（x）＞0；
∴f（x）在R上是增函数；
（2）由原不等式得：f（1-m）＜f（m2-1）；
∵f（x）在（-2，2）上是增函数，所以：
|
| 3 |
∴实数m的取值范围是(1，
| 3 |
点评：考查函数导数符号和函数单调性的关系，根据函数单调性解不等式．
练习册系列答案
相关题目
函数f（x）=log2（x+4）-3x的零点有（ ）
| A、0 | B、1 | C、2 | D、3 |
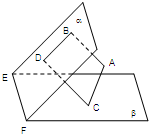如图，设平面α∩平面β=EF，AB⊥α，CD⊥α，垂足分别为B，D，如果再增加一个条件，就可以推出BD⊥EF．现有：①AC⊥β；②AC∥EF；③AC与CD在β内的射影在同一条直线上．那么上述三个条件中能成为增加条件的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
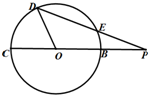如图，割线PBC经过圆心O，OB=PB=1，又PED交圆O于E，D，且DE=设f（n）=2+24+27+210+…+23n+10（n∈N），则f（n）等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|