题目内容
7.若函数y=x2-2mx+1在(-∞,1)上是单调递减函数,则实数m的取值范围[1,+∞).分析 利用函数的单调性和对称轴之间的关系,确定区间和对称轴的位置,从而建立不等式关系,进行求解即可.
解答 解:y=x2-2mx+1的对称轴为x=-$\frac{-2m}{2}$=m,
函数f(x)在(-∞,m]上单调递减,
∵函数y=x2-2mx+1在(-∞,1)上是单调递减函数,
∴对称轴m≥1.
即m的取值范围是[1,+∞).
故答案为:[1,+∞).
点评 本题主要考查二次函数的图象和性质,利用二次函数单调性由对称轴决定,从而得到对称轴与已知区间的关系是解决本题的关键,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.安排一张有5个独唱节目和3个合唱节目的节目单,要求任何2个合唱节目不相邻而且不排在第一个节目,那么不同的节目单有( )
| A. | 7200种 | B. | 1440种 | C. | 1200种 | D. | 2880种 |
19.已知扇形的弧长是4cm,面积是2cm2,则扇形的圆心角的弧度数是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 1或4 |
16.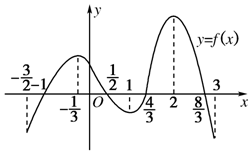 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )| A. | $[{-\frac{1}{3},1}]∪[2,3]$ | B. | $[{-1,\frac{1}{2}}]∪[{\frac{4}{3},\frac{8}{3}}]$ | ||
| C. | $[{-\frac{3}{2},\frac{1}{2}}]∪[1,2)$ | D. | $[{-\frac{3}{2},-\frac{1}{3}}]∪[{\frac{1}{2},\frac{4}{3}}]∪[{\frac{4}{3},3}]$ |
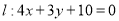 ,半径为
,半径为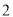 的圆
的圆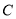 与
与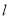 相切,圆心
相切,圆心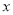 轴上且在直线
轴上且在直线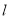 的右上方.
的右上方.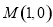 且与圆
且与圆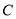 交于
交于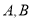 两点(
两点(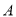 在
在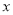 轴上方,B在
轴上方,B在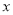 轴正半轴上是否存在定点
轴正半轴上是否存在定点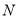 ,使得
,使得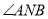 ?若存在,请求出点
?若存在,请求出点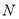 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.