题目内容
16.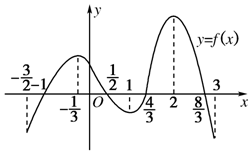 函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )| A. | $[{-\frac{1}{3},1}]∪[2,3]$ | B. | $[{-1,\frac{1}{2}}]∪[{\frac{4}{3},\frac{8}{3}}]$ | ||
| C. | $[{-\frac{3}{2},\frac{1}{2}}]∪[1,2)$ | D. | $[{-\frac{3}{2},-\frac{1}{3}}]∪[{\frac{1}{2},\frac{4}{3}}]∪[{\frac{4}{3},3}]$ |
分析 根据导数大于0时函数单调递增,导数小于0时原函数单调递减确定函数f(x)的单调性
解答 解:由图象可知,即求函数的单调减区间,
从而有解集为[-$\frac{1}{3}$,1]∪[2,3],
故选:A.
点评 本题主要考查了函数的单调性与导数的关系,解题的关键是识图,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}$|=ad-bc,则符合条件$|{\begin{array}{l}z&{1+2i}\\{1-2i}&{1-i}\end{array}}$|=0的复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.不等式|x+1|≥kx对任意的x∈R均成立,则k的取值范围是( )
| A. | (-∞,0) | B. | [-1,0] | C. | [0,1] | D. | [0,+∞) |
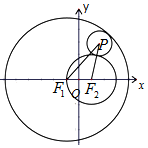 已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.
已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.