题目内容
18.已知方程$\frac{x^2}{2-k}+\frac{y^2}{3+k}=1$表示椭圆,求实数k的取值范围-3<m<2且x≠-$\frac{1}{2}$.分析 根据题意,由椭圆的标准方程分析可得$\left\{\begin{array}{l}{2-k>0}\\{3+k>0}\\{2-k≠3+k}\end{array}\right.$,解可得k的取值范围,即可得答案.
解答 解:根据题意,方程$\frac{x^2}{2-k}+\frac{y^2}{3+k}=1$表示椭圆,
则有$\left\{\begin{array}{l}{2-k>0}\\{3+k>0}\\{2-k≠3+k}\end{array}\right.$,
解可得:-3<m<2且x≠-$\frac{1}{2}$,
故答案为:-3<m<2且x≠-$\frac{1}{2}$.
点评 本题考查椭圆的标准方程,注意与圆的标准方程的区分.

练习册系列答案
相关题目
11.不等式|x+1|≥kx对任意的x∈R均成立,则k的取值范围是( )
| A. | (-∞,0) | B. | [-1,0] | C. | [0,1] | D. | [0,+∞) |
13.某地市高三理科学生有30000名,在一次调研测试中,数学成绩ξ~N(100,σ2),已知P(80<ξ≤100)=0.45,若按分层抽样的方式取200份试卷进行成绩分析,则应从120分以上的试卷中抽取( )
| A. | 5份 | B. | 10份 | C. | 15份 | D. | 20份 |
7.若随机变量X服从正态分布N(1,4),设P(0<X<3)=m,P(-1<X<2)=n,则m、n的大小关系为( )
| A. | m>n | B. | m<n | C. | m=n | D. | 不确定 |
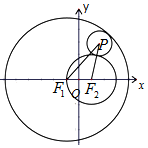 已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.
已知定圆C1:(x+1)2+y2=36及定圆C2:(x-1)2+y2=4,动圆P与C1内切,与C2外切,求动圆圆心P的轨迹方程.