题目内容
19.在平行四边形ABCD中,AB=4,AD=2,∠A=$\frac{π}{3}$,M为DC的中点,N为平面ABCD内一点,若|$\overrightarrow{AB}$-$\overrightarrow{NB}$|=|$\overrightarrow{AM}$-$\overrightarrow{AN}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$=( )| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
分析 根据条件及向量加减法的几何意义即可得出|$\overrightarrow{AN}$|=|$\overrightarrow{MN}$|,再根据向量的数量积公式计算即可
解答 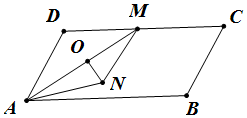 解:由|$\overrightarrow{AB}$-$\overrightarrow{NB}$|=|$\overrightarrow{AM}$-$\overrightarrow{AN}$|,可得|$\overrightarrow{AN}$|=|$\overrightarrow{MN}$|,
解:由|$\overrightarrow{AB}$-$\overrightarrow{NB}$|=|$\overrightarrow{AM}$-$\overrightarrow{AN}$|,可得|$\overrightarrow{AN}$|=|$\overrightarrow{MN}$|,
取AM的中点为O,连接ON,则ON⊥AM,
又$\overrightarrow{AM}$=$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$,
所以$\overrightarrow{AM}$•$\overrightarrow{AN}$=$\frac{1}{2}$${\overrightarrow{AM}}^{2}$=$\frac{1}{2}$($\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$)2=$\frac{1}{2}$(${\overrightarrow{AD}}^{2}$+$\frac{1}{4}$${\overrightarrow{AB}}^{2}$+$\overrightarrow{AD}$•$\overrightarrow{AB}$)=$\frac{1}{2}$(4+$\frac{1}{4}$×16+2×4×$\frac{1}{2}$)=6,
故选:D.
点评 本题主要考查了平面向量的几何表示,数量积的几何意义,运算求解能力,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
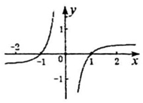
11.设曲线y=1nx在x=2处的切线与直线ax+y+1=0垂直,则a的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
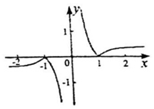
8.已知函数f(x)=x2,g(x)=-1nx,g'(x)为g(x)的导函数.若存在直线l同为函数f(x)与g'(x)的切线,则直线l的斜率为( )
| A. | $2\sqrt{5}-4$ | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |


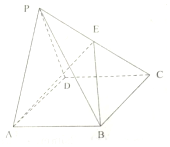 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.