题目内容
6.已知公差不为0的等差数列{an}与等比数列$\{{b_n}\},{a_1}=2,{b_n}={a_{2^n}}$,则{bn}的前5项的和为( )| A. | 142 | B. | 124 | C. | 128 | D. | 144 |
分析 b1=a2=2+d,b2=a4=2+3d,b3=a8=2+7d,利用(2+3d)2=(2+d)(2+7d),d≠0,解得d.即可得出公比q,再利用求和公式即可得出.
解答 解:b1=a2=2+d,b2=a4=2+3d,b3=a8=2+7d,
则(2+3d)2=(2+d)(2+7d),d≠0,解得d=2.
∴b1=4,b2=8,公比q=2.
∴{bn}的前5项的和=$\frac{4×({2}^{5}-1)}{2-1}$=124.
故选:B.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)=2g(x)+$\frac{x-4}{{x}^{2}+1}$,若f($\frac{1}{sinθ}$)+f(cos2θ)<f(π)-f($\frac{1}{π}$),则θ的取值范围是( )
| A. | (2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$),k∈Z | |
| B. | (2kπ-$\frac{π}{6}$,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+$\frac{7}{6}$π),k∈Z | |
| C. | (2kπ-$\frac{5π}{6}$,2kπ-$\frac{π}{6}$),k∈Z | |
| D. | (2kπ-$\frac{7π}{6}$,2kπ-π)∪(2kπ-π,2kπ)∪(2kπ,2kπ+$\frac{π}{6}$),k∈Z |
1.已知集合P={x|x2-2x-8≤0},Q={x|x≥a},(∁RP)∪Q=R,则a的取值范围是( )
| A. | (-2,+∞) | B. | (4,+∞) | C. | (-∞,-2] | D. | (-∞,4] |
11.设曲线y=1nx在x=2处的切线与直线ax+y+1=0垂直,则a的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
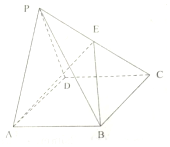 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.