题目内容
2.已知a,b,c为正实数,求证:$\frac{b^2}{a}+\frac{c^2}{b}+\frac{a^2}{c}≥a+b+c$.分析 不等式两边同时加上a+b+c,分组使用基本不等式即可得出结论.
解答 证明:∵a,b,c为正实数,
∴a+$\frac{{b}^{2}}{a}$≥2b,b+$\frac{{c}^{2}}{b}$≥2c,c+$\frac{{a}^{2}}{c}$≥2a,
将上面三个式子相加得:
a+b+c+$\frac{{b}^{2}}{a}+\frac{{c}^{2}}{b}+\frac{{a}^{2}}{c}$≥2a+2b+2c,
∴$\frac{{b}^{2}}{a}+\frac{{c}^{2}}{b}+\frac{{a}^{2}}{c}$≥a+b+c.
点评 本题考查了不等式的证明,基本不等式的应用,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}{2^{1-|x|}},x≤1\\-{(x-2)^2},x>1\end{array}\right.$,若$f(m)=\frac{1}{4}$,则f(1-m)=( )
| A. | -1 | B. | -4 | C. | -9 | D. | -16 |
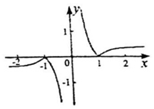
11.设曲线y=1nx在x=2处的切线与直线ax+y+1=0垂直,则a的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
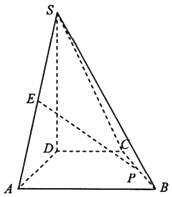 如图,在四棱锥S-ABCD中,SD⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=∠DAB=90°,SD=AD=AB=2,DC=1
如图,在四棱锥S-ABCD中,SD⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=∠DAB=90°,SD=AD=AB=2,DC=1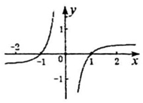


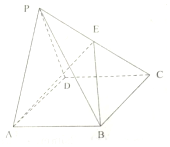 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.