题目内容
9.已知函数f(x)=$\sqrt{3}sinxcosx+{sin^2}$x.(Ⅰ)求函数f(x)的递增区间;
(Ⅱ)△ABC的角A,B,C所对边分别是a,b,c,角A的平分线交BC于D,f(A)=$\frac{3}{2}$,AD=$\sqrt{2}$BD=2,求cosC.
分析 (Ⅰ)利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的单调性,求得函数f(x)的递增区间.
(Ⅱ)在△ABC中,利用正弦定理求得sinB的值,可得B的值,再利用两角和的余弦公式,求得cosC=-cos(A+B)的值.
解答 解:(Ⅰ)$f(x)=\sqrt{3}sinxcosx+{sin^2}x$=$\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x+\frac{1}{2}=sin(2x-\frac{π}{6})+\frac{1}{2}$,
令 $2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2},k∈Z$,解得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3},k∈z$,
所以递增区间是$[kπ-\frac{π}{6},kπ+\frac{π}{3}](k∈z)$.
(Ⅱ)$f(A)=\frac{3}{2}⇒sin(2A-\frac{π}{6})=1$,得到$2A-\frac{π}{6}=2kπ+\frac{π}{2}⇒A=kπ+\frac{π}{3},k∈z$,
由$0<A<\frac{π}{2}$,得到$A=\frac{π}{3}$,所以角$∠BAD=\frac{π}{6}$,
由正弦定理得$\frac{BD}{sin∠BAD}$=$\frac{AD}{sinB}$,∴sinB=$\frac{\sqrt{2}}{2}$,∴$B=\frac{π}{4}$,
∴$cosC=-cos(A+B)=sin\frac{π}{3}sin\frac{π}{4}-cos\frac{π}{3}cos\frac{π}{4}=\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
点评 本题主要考查三角恒等变换,正弦函数的单调性,正弦定理、两角和的余弦公式的应用,属于基础题.

 阅读快车系列答案
阅读快车系列答案(I)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天收入不低于300元的概率.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | (-∞,e) | B. | (-∞,e] | C. | $(-∞,\frac{1}{e})$ | D. | $(-∞,\frac{1}{e}]$ |
| A. | (-2,+∞) | B. | (4,+∞) | C. | (-∞,-2] | D. | (-∞,4] |
| A. | (0,3] | B. | (0,4] | C. | [2,3] | D. | [2,+∞) |
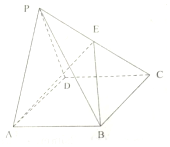 如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.
如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,△PAD为正三角形,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l.