题目内容
17.在△ABC中,B=45°,C=60°,c=2,则b=( )| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{3\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由已知利用正弦定理即可计算得解.
解答 解:∵B=45°,C=60°,c=2,
∴b=$\frac{c•sinB}{sinC}$=$\frac{2×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{6}}{3}$.
故选:A.
点评 本题主要考查了正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
8.我们常用函数y=f(x)的函数值的改变量与自变量的改变量的比值来表示平均变化率,当自变量x由x0改变到x+x0时,函数值的改变量△y等于( )
| A. | f(x0+△x) | B. | f(x0)+△x | C. | f(x0)•△x | D. | f(x0+△x)-f(x0) |
9.已知变量x和y满足关系$\widehat{y}$=0.7x+0.35,变量y与z负相关,下列结论中正确的是( )
| A. | x与y正相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y负相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
4.执行如图所示的程序框图,若输入的a=5,则输出的结果是( )
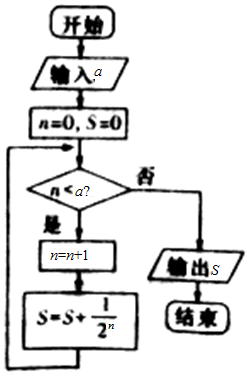

| A. | $\frac{15}{16}$ | B. | $\frac{31}{16}$ | C. | $\frac{31}{32}$ | D. | $\frac{63}{32}$ |

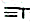 ”表示36,“
”表示36,“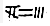 ”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )
”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )


 如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.
如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.