题目内容
7．已知z1=1-i，z2=2+2i．（1）求z1•z2；
（2）若z=$\frac{{z}_{1}•{z}_{2}}{{z}_{1}+{z}_{2}}$，求z．
分析 直接利用复数代数形式的乘法运算化简得答案．
解答 解：（1）z1=1-i，z2=2+2i则z1•z2=（1-i）（2+2i）=4，
（2）z1+z2=1-i+2+2i=3+i，
∴z=$\frac{{z}_{1}•{z}_{2}}{{z}_{1}+{z}_{2}}$=$\frac{4}{3+i}$=$\frac{4（3-i）}{（3+i）（3-i）}$=$\frac{6-2i}{5}$
点评 本题考查了复数代数形式的乘法运算，是基础题．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
17．若单位向量$\overrightarrow{e_1}$，$\overrightarrow{e_2}$的夹角为$\frac{π}{3}$，则向量$\overrightarrow{e_1}-2\overrightarrow{e_2}$与向量$\overrightarrow{e_1}$的夹角为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
18．集合M={（x，y）|x+y≤1，y≤x，y≥-1}，N={（x，y）|（x-2）2+y2=r2，r＞0}，若M∩N≠∅，则r的取值范围为（ ）
| A． | $[{\frac{{\sqrt{2}}}{2}，3}]$ | B． | $[{1，\sqrt{10}}]$ | C． | $[{\frac{{\sqrt{2}}}{2}，\sqrt{10}}]$ | D． | $[{1，\frac{{\sqrt{10}}}{2}}]$ |
2．已知复数z=3+4i，则|z|等于（ ）
| A． | 25 | B． | 12 | C． | 7 | D． | 5 |
19．在△ABC中，a，b，c分别为角A，B，C所对的边，若b=$\sqrt{2}$，a=2，B=$\frac{π}{4}$，则c=（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{3}$ |
16．
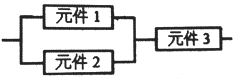某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为$\frac{1}{2}$），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（ ）
某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为$\frac{1}{2}$），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，502），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{5}{8}$ | D． | $\frac{3}{8}$ |
17．在△ABC中，B=45°，C=60°，c=2，则b=（ ）
| A． | $\frac{{2\sqrt{6}}}{3}$ | B． | $\frac{{3\sqrt{6}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |