题目内容
3. 如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.
如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.
分析 由约束条件作出可行域,然后对m分类讨论求得满足条件的m的值.
解答 解:由约束条件$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$作出可行域如图,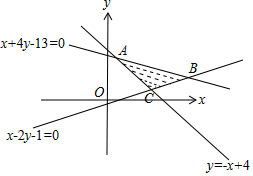
若m=0,目标函数为z=x,有最小值的点仅有A点,不合题意;
若m>0,化目标函数z=x+my为y=-$\frac{1}{m}x+\frac{z}{m}$,由图可知,线段AC上的点均满足题意,
联立$\left\{\begin{array}{l}{y=-x+4}\\{x-2y-1=0}\end{array}\right.$,解得C(3,1),
联立$\left\{\begin{array}{l}{y=-x+4}\\{x+4y-13=0}\end{array}\right.$,解得A(1,3),
此时$-\frac{1}{m}={k}_{AC}=-1$,得m=1;
若m<0,化目标函数z=x+my为y=-$\frac{1}{m}x+\frac{z}{m}$,由图可知,满足目标函数取得最小值的点仅有A点,不合题意.
∴满足条件的m值为1.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.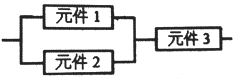 某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
 某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为$\frac{1}{2}$),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
17.在△ABC中,B=45°,C=60°,c=2,则b=( )
| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{3\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
14.若实数a,b,c满足对任意实数x,y有3x+4y-5≤ax+by+c≤3x+4y+5,则( )
| A. | a+b-c的最小值为2 | B. | a-b+c的最小值为-4 | ||
| C. | a+b-c的最大值为4 | D. | a-b+c的最大值为6 |
1.在测试中,客观题难度的计算公式为${P_i}=\frac{R_i}{N}$,其中Pi为第i题的难度,Ri为答对该题的人数,N为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:
测试后,随机抽取了20名学生的答题数据进行统计,结果如下:
(Ⅰ)根据题中数据,估计这240名学生中第5题的实测答对人数;
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为X,求X的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设${P_i}^′$为第i题的实测难度,请用Pi和${P_i}^′$设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度Pi | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 实测答对人数 | 16 | 16 | 14 | 14 | 4 |
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为X,求X的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设${P_i}^′$为第i题的实测难度,请用Pi和${P_i}^′$设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
15.在△ABC中,关于x的方程(1+x2)sinA+2xsinB+(1-x2)sinC=0无实数根,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等边三角形 |
12.已知a是平面α外的一条直线,过a作平面β,使β∥α,这样的β( )
| A. | 恰能作一个 | B. | 至多能作一个 | C. | 至少能作一个 | D. | 不存在 |
13.在(x-4)5的展开式中,含x3的项的系数为( )
| A. | 20 | B. | 40 | C. | 80 | D. | 160 |