题目内容

2．已知数列{an}，a1=1且点（an，an+1）在函数y=2x+1的图象上，则a4=15．

分析 根据点在直线上建立条件关系即可得到结论．

解答 解：∵点（an，an+1）在函数y=2x+1的图象上，
∴2an+1=an+1，
∵a1=1，
∴a2=2a1+1=3，
a3=2a2+1=7，
a4=2a3+1=15，
故答案为：15

点评 本题主要考查数列的函数性质，根据条件得到一个递推数列是解决本题的关键．

练习册系列答案
相关题目
12．过双曲线x2-y2=1焦点的直线垂直于x轴，交双曲线于A、B两点，则|AB|=2．
13．在等差数列{an}中，a7a11=6，a4+a14=5，则该数列公差d等于（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$或$-\frac{1}{2}$C．-$\frac{1}{4}$D．$\frac{1}{4}$或-$\frac{1}{4}$
10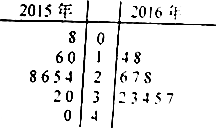．随机抽取某篮球运动员2015年和2016年各10场篮球赛投篮得分X，得到如图所示X的茎叶图．$\overline{X}$2015、$\overline{X}$2016与S22015、S22016是分别是2015年和2016年X的平均数与方差，由图可知（　　）
A．$\overline{X}$2015＞$\overline{X}$2016，S22015＞S22016B．$\overline{X}$2015＞$\overline{X}$2016，S22015＜S22016
C．$\overline{X}$2015＜$\overline{X}$2016，S22015＜S22016D．$\overline{X}$2015＜$\overline{X}$2016，S22015＞S22016
17．在△ABC中，B=45°，C=60°，c=2，则b=（　　）
A．$\frac{{2\sqrt{6}}}{3}$B．$\frac{{3\sqrt{6}}}{2}$C．$\frac{1}{2}$D．$\frac{{\sqrt{3}}}{2}$
7．已知条件p：x≥a，q：{x|x＜-3或x＞3}，若p是q的充分不必要条件，则实数a的取值范围是（3，+∞）．
14．若实数a，b，c满足对任意实数x，y有3x+4y-5≤ax+by+c≤3x+4y+5，则（　　）
A．a+b-c的最小值为2B．a-b+c的最小值为-4
C．a+b-c的最大值为4D．a-b+c的最大值为6
8．已知$\overrightarrow{m}$=（2cosx+2$\sqrt{3}$sinx，1），$\overrightarrow{n}$=（cosx，-y），且$\overrightarrow{m}$⊥$\overrightarrow{n}$．
（Ⅰ）将y表示x的函数f（x），并求f（x）的单调增区间；
（Ⅱ）已知a，b，c分别为△ABC的三个内角A，B，C对应的边长，若f（$\frac{A}{2}$）=3，且a=3，b+c=4，求△ABC的面积．
9．已知数列{an}的前n项和为Sn，且2，Sn，an成等差数列，则S17=（　　）
A．0B．2C．-2D．34

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网