题目内容
已知函数f(x)=ex+
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)若对所有x≤0都有f(x)≥ax+1,求实数a的取值范围.
| 1 |
| ex |
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)若对所有x≤0都有f(x)≥ax+1,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)利用导数判断函数的单调性,进而可求出函数的最小值;
(Ⅱ)令g(x)=f(x)-ax-1=e-x+(e-a)x-1,即g(x)≥g(0)=0成立,分类讨论并利用导数判断函数的单调性,即可得出结论.
(Ⅱ)令g(x)=f(x)-ax-1=e-x+(e-a)x-1,即g(x)≥g(0)=0成立,分类讨论并利用导数判断函数的单调性,即可得出结论.
解答:
解:(Ⅰ)由已知得f'(x)=-e-x+e,…(1分)
令f'(x)>0得x>-1;令f'(x)<0得x<-1.
因此,函数f (x)在(-∞,-1]上单调减函数,在[-1,+∞)上是单调增函数,…(5分)
当x=-1时,f(x)的有极小值也是最小值,f(x)min=0…(6分)
(Ⅱ)令g(x)=f(x)-ax-1=e-x+(e-a)x-1,
则g'(x)=-e-x+(e-a),g(0)=0.…(8分)
(1)当e-a≤0,即a≥e时,g'(x)=-e-x+(e-a)<0,g(x)在(-∞,0]是减函数,
因此当x≤0时,都有g(x)≥g(0)=0,即f(x)-ax-1≥0,f(x)≥ax+1;…(10分)
(2)当a<e时,令g'(x)<0得x<-ln(e-a);令g'(x)>0得x>-ln(e-a),
因此函数g(x)在(-∞,-ln(e-a)]上是减函数,在[-ln(e-a),+∞)上是增函数.
由于对所有x≤0都有f(x)≥ax+1,即g(x)≥g(0)=0成立,
因此-ln(e-a)≥0,e-a≤1,a≥e-1,又a<e,
所以e-1≤a≤e.…(13分)
综上所述,a的取值范围是[e-1,+∞).…(14分)
令f'(x)>0得x>-1;令f'(x)<0得x<-1.
因此,函数f (x)在(-∞,-1]上单调减函数,在[-1,+∞)上是单调增函数,…(5分)
当x=-1时,f(x)的有极小值也是最小值,f(x)min=0…(6分)
(Ⅱ)令g(x)=f(x)-ax-1=e-x+(e-a)x-1,
则g'(x)=-e-x+(e-a),g(0)=0.…(8分)
(1)当e-a≤0,即a≥e时,g'(x)=-e-x+(e-a)<0,g(x)在(-∞,0]是减函数,
因此当x≤0时,都有g(x)≥g(0)=0,即f(x)-ax-1≥0,f(x)≥ax+1;…(10分)
(2)当a<e时,令g'(x)<0得x<-ln(e-a);令g'(x)>0得x>-ln(e-a),
因此函数g(x)在(-∞,-ln(e-a)]上是减函数,在[-ln(e-a),+∞)上是增函数.
由于对所有x≤0都有f(x)≥ax+1,即g(x)≥g(0)=0成立,
因此-ln(e-a)≥0,e-a≤1,a≥e-1,又a<e,
所以e-1≤a≤e.…(13分)
综上所述,a的取值范围是[e-1,+∞).…(14分)
点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,考查学生恒成立问题的等价转化思想及分类讨论思想的运用能力,属于难题.

练习册系列答案
相关题目
A,B,C为△ABC三内角,则“cosA+sinA=cosB+sinB”是“∠C=90°”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
当x>0时,函数f(x)=
+3x的最小值是( )
| 12 |
| x |
| A、10 | B、11 | C、12 | D、13 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直线l1:x+ay+6=0和l2:(a-2)x+3y+2a=0,则l1∥l2时,a的值为( )
| A、a=3,a=-1 |
| B、a=3 |
| C、a=-1 |
| D、以上都不对 |
某人忘记了电话号码的最后一个数字,随意拨号,则拨号不超过3次而接通电话的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
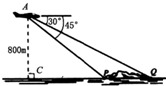 某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).
某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).