题目内容
已知直线l1：x+ay+6=0和l2：（a-2）x+3y+2a=0，则l1∥l2时，a的值为（ ）
| A、a=3，a=-1 |
| B、a=3 |
| C、a=-1 |
| D、以上都不对 |
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：利用两条直线平行与斜率的关系即可得出．
解答：
解：∵直线l2的斜率存在，l1∥l2，
∴kl1=kl2．
∴-
=
，化为a2-2a-3=0．
解得a=3或-1．
当a=3时，l1与l2重合，应舍去．
∴a=-1．
故选：C．
∴kl1=kl2．
∴-
| 1 |
| a |
| 2-a |
| 3 |
解得a=3或-1．
当a=3时，l1与l2重合，应舍去．
∴a=-1．
故选：C．
点评：本题考查了两条直线平行与斜率的关系，属于基础题．
练习册系列答案
相关题目
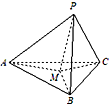如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=2．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（已知椭圆
+
=1（a＞b＞0），F为左焦点，A为左顶点，B为上顶点，C为下顶点，且
•
=0，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| CF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0|）的图象如下图所示，则f（1）+f（2）+f（3）+…+f（2014）=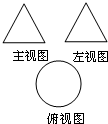
（文科）一个几何体的三视图如图所示，其中主视图和左视图是全等的正三角形，且该几何体的表面积为3π，则该几何体的体积为