题目内容

当x＞0时，函数f（x）=
12
x
+3x的最小值是（　　）
A、10B、11C、12D、13
考点：基本不等式在最值问题中的应用
专题：不等式的解法及应用
分析：本题可直接利用积为定值，求和的最小值，得本题结论．
解答： 解：∵x＞0，
∴f（x）=
12
x
+3x≥2
12
x
•3x
=12，
当且仅当
12
x
=3x，即x=2时取等号．
故选：C．
点评：本题考查的是基本不等式，注意不等式的使用条件，本题思维量小，计算量也不大，属于基础题．
练习册系列答案
相关题目
已知数列{an}的前n项和为Sn，且有a1=2，3Sn=5an-an-1+3Sn-1（n≥2）．
（1）求数列{an}的通项公式；
（2）若bn=（2n-1）an，求数列{bn}的前n项和Tn；
（3）若
3
2
m2+m≤bn，对所有n∈N+都成立，求m的取值范围．
若方程
2x-x2
=kx-2k+2有两个不同的实数根，则实数k的取值范围是
 
．
10件产品中有3件是次品，现任取2件，其中最多有1件是次品的概率是
 
（用古典概率解）．
已知函数f（x）=（x-p）|x-p|+tlnx（t＜0，p≥0），
（Ⅰ）当t=-1，p=0时，求函数f（x）的极值；
（Ⅱ）当p=
1
2
 ， t=-
3
2
时，求函数f（x）的单调区间；
（Ⅲ）当p=
t
2
+1时，若f（x）≥
1
9
对于x∈（p，+∞）时恒成立，求实数t的取值范围．
数列{an}满足an+1+an=2n-3，若a1=2则a21-a20=（　　）
A、9B、7C、5D、3
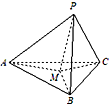如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=2．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（
1
3
，x，y），则x+y=
 
．
已知函数f（x）=ex+
1
ex

（Ⅰ）求函数f（x）的最小值；
（Ⅱ）若对所有x≤0都有f（x）≥ax+1，求实数a的取值范围．
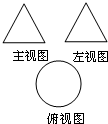（文科）一个几何体的三视图如图所示，其中主视图和左视图是全等的正三角形，且该几何体的表面积为3π，则该几何体的体积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网