题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:抛物线的简单性质,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线的渐近线的方程可得
=
,再利用抛物线的准线x=-6=-c及c2=a2+b2即可得出.
| b |
| a |
| 3 |
解答:
解:∵双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,
∴
=
,
∵双曲线的一个焦点在抛物线y2=24x的准线x=-6上,
∴c=6.
联立
,
解得
.
∴此双曲线的方程为
-
=1,
故选D.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴
| b |
| a |
| 3 |
∵双曲线的一个焦点在抛物线y2=24x的准线x=-6上,
∴c=6.
联立
|
解得
|
∴此双曲线的方程为
| x2 |
| 9 |
| y2 |
| 27 |
故选D.
点评:本题考查的知识点是抛物线的简单性质和双曲线的简单性质,熟练掌握圆锥曲线的图象和性质是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
数列{an}满足an+1+an=2n-3,若a1=2则a21-a20=( )
| A、9 | B、7 | C、5 | D、3 |
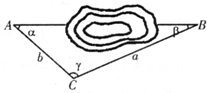 如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )
如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )| A、a,b,γ |
| B、a,b,α |
| C、a,b,β |
| D、α,β,a |
已知坐标原点O在圆x2+y2-x+y+m=0外,则m的取值范围是( )
A、0<m<
| ||
B、m<
| ||
C、m≤
| ||
| D、m>0 |
 已知点
已知点 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=