题目内容
已知y=f(x)是偶函数,定义x≥0时,f(x)=
(1)求f(-2);
(2)当x<-3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[-5,5]上的最大值为g(a),试求g(a)的表达式.
|
(1)求f(-2);
(2)当x<-3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[-5,5]上的最大值为g(a),试求g(a)的表达式.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)已知y=f(x)是偶函数,故f(-2)=f(2)=2(3-2)=2;
(2)当x<-3时,f(x)=f(-x)=(-x-3)(a+x)=-(x+3)(a+x),
(3)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,在这两段上分别研究二次函数的区间上的最值即可.
(2)当x<-3时,f(x)=f(-x)=(-x-3)(a+x)=-(x+3)(a+x),
(3)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,在这两段上分别研究二次函数的区间上的最值即可.
解答:
解:(1)已知y=f(x)是偶函数,故f(-2)=f(2)=2(3-2)=2;
(2)当x<-3时,f(x)=f(-x)=(-x-3)(a+x)=-(x+3)(a+x),
所以,当x<-3时,f(x)的解析式为f(x)=-(x+3)(a+x)
(3)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,
①当a≤3时,f(x)在[0,
]上单调递增,在[
,+∞)上单调递减,所以g(a)=f(
)=
,
②当3<a≤7时,f(x)在[0,
]与[3,
]上单调递增,在[
,3]与[
,5]上单调递减,
所以此时只需比较f(
)=
与f(
)=
的大小.
(A)当3<a≤6时,f(
)=
≥f(
)=
,所以g(a)=f(
)=
(B)当6<a≤7时,f(
)=
<f(
)=
,所以g(a)=f(
)=
③当a>7时,f(x)在[0,
]与[3,5]上单调递增,在[
,3]上单调递减,且f(
)=
<f(5)=2(a-5),所以g(a)=f(5)=2(a-5),
综上所述,g(a)=
(2)当x<-3时,f(x)=f(-x)=(-x-3)(a+x)=-(x+3)(a+x),
所以,当x<-3时,f(x)的解析式为f(x)=-(x+3)(a+x)
(3)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,
①当a≤3时,f(x)在[0,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
②当3<a≤7时,f(x)在[0,
| 3 |
| 2 |
| 3+a |
| 2 |
| 3 |
| 2 |
| 3+a |
| 2 |
所以此时只需比较f(
| 3 |
| 2 |
| 9 |
| 4 |
| 3+a |
| 2 |
| (a-3)2 |
| 4 |
(A)当3<a≤6时,f(
| 3 |
| 2 |
| 9 |
| 4 |
| 3+a |
| 2 |
| (a-3)2 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
(B)当6<a≤7时,f(
| 3 |
| 2 |
| 9 |
| 4 |
| 3+a |
| 2 |
| (a-3)2 |
| 4 |
| 3+a |
| 2 |
| (a-3)2 |
| 4 |
③当a>7时,f(x)在[0,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
综上所述,g(a)=
|
点评:本题主要考查函数的值域求法,综合考查了分段函数求值域的问题,特别对于二次函数求值域时要分类讨论的思想.

练习册系列答案
相关题目
已知坐标原点O在圆x2+y2-x+y+m=0外,则m的取值范围是( )
A、0<m<
| ||
B、m<
| ||
C、m≤
| ||
| D、m>0 |
函数f(x)=ax2+bx+5满足条件f(-1)=f(3),则f(2)的值为( )
| A、5 | B、6 |
| C、8 | D、与a,b的值有关 |
 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=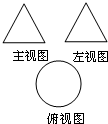 (文科)一个几何体的三视图如图所示,其中主视图和左视图是全等的正三角形,且该几何体的表面积为3π,则该几何体的体积为
(文科)一个几何体的三视图如图所示,其中主视图和左视图是全等的正三角形,且该几何体的表面积为3π,则该几何体的体积为