题目内容
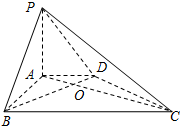 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB⊥AD,AC与BD交于点O,PA=3,AD=2,AB=2
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB⊥AD,AC与BD交于点O,PA=3,AD=2,AB=2| 3 |
(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)求直线PO与平面PAB所成的角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)在Rt△ABC中,利用已知可得∠BAC=60°,同理可得∠ABD=30°,进而得到BD⊥AC,利用侧面垂直的性质可得PA⊥BD,利用线面垂直的判定定理即可得出;
(Ⅱ)过O作OE⊥AB交AB于E,则OE⊥平面PAB,所以∠OPE是直线PO与平面PAB所成的角,求出OE,PO,即可求直线PO与平面PAB所成的角的正弦值.
(Ⅱ)过O作OE⊥AB交AB于E,则OE⊥平面PAB,所以∠OPE是直线PO与平面PAB所成的角,求出OE,PO,即可求直线PO与平面PAB所成的角的正弦值.
解答:
(Ⅰ) 证明:因为AD∥BC,AB⊥AD,AD=2,AB=2
,
所以tan∠ABD=
即∠ABD=30°.
又在直角△ABC中,tan∠BAC=
,所以∠BAC=
.
所以BD⊥AC
又因为PA⊥平面ABCD,所以BD⊥PA.
所以BD⊥平面PAC;…(7分)
(Ⅱ)解:过O作OE⊥AB交AB于E,则OE⊥平面PAB,所以∠OPE是直线PO与平面PAB所成的角…(11分)
又在直角△ABO中,∠BAC=
,AB=2
,则OE=
,AO=
.
又在直角△PAO中,AO=
,AP=3,所以PO=2
.
所以sin∠OPE=
.
所以直线PO与平面PAB所成的角的正弦值为
.…(14分)
| 3 |
所以tan∠ABD=
| ||
| 3 |
又在直角△ABC中,tan∠BAC=
| 3 |
| π |
| 3 |
所以BD⊥AC
又因为PA⊥平面ABCD,所以BD⊥PA.
所以BD⊥平面PAC;…(7分)
(Ⅱ)解:过O作OE⊥AB交AB于E,则OE⊥平面PAB,所以∠OPE是直线PO与平面PAB所成的角…(11分)
又在直角△ABO中,∠BAC=
| π |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
又在直角△PAO中,AO=
| 3 |
| 3 |
所以sin∠OPE=
| ||
| 4 |
所以直线PO与平面PAB所成的角的正弦值为
| ||
| 4 |
点评:本题主要考查空间点、线、面位置关系,线面所成角等基础知识,同时考查空间想象能力和推理论证能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
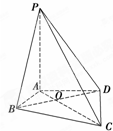 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点. 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2, 如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.