题目内容
数列{an}的通项公式为an=2n-1,数列{bn}是等差数列且 b1=a1,b4=a1+a2+a3.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)设Cn=
,数列{cn}的前n项和为Tn,证明:Tn<
.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)设Cn=
| 1 |
| bnbn+1 |
| 1 |
| 2 |
考点:数列的求和
专题:证明题,等差数列与等比数列
分析:(Ⅰ)设数列{bn}的公差为d,依题意,可求得b1=a1=1,b4=1+3d=7,从而可求得d及数列{bn}的通项公式;
(Ⅱ)利用裂项法易知cn=
=
=
(
-
),从而可求Tn=
(1-
),继而可证结论成立.
(Ⅱ)利用裂项法易知cn=
| 1 |
| bnbn+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
解答:
解:(I)设数列{bn}的公差为d,又an=2n-1
∴b1=a1=1,b4=1+3d=a1+a2+a3=1+2+4=7,
∴d=2,
∴bn=1+(n-1)×2=2n-1------------(5分)
(II)cn=
=
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
)=
(1-
)=
,
∵n∈N*,∴Tn=
(1-
)<
------------(12分)
∴b1=a1=1,b4=1+3d=a1+a2+a3=1+2+4=7,
∴d=2,
∴bn=1+(n-1)×2=2n-1------------(5分)
(II)cn=
| 1 |
| bnbn+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
∵n∈N*,∴Tn=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
点评:本题考查数列的求和,着重考查等差数列的通项公式及裂项法求和,考查运算能力,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
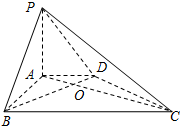 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB⊥AD,AC与BD交于点O,PA=3,AD=2,AB=2
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB⊥AD,AC与BD交于点O,PA=3,AD=2,AB=2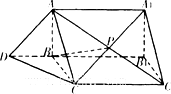 直三棱柱ABC-A1B1C1中,AB⊥BC,BC=
直三棱柱ABC-A1B1C1中,AB⊥BC,BC=