题目内容
如图，在三棱锥P-ABC中，平面PAC⊥平面ABC，PD⊥AC于点D，且DC=2AD=2，E为PC上一点，PE：EC=1：2，（Ⅰ）求证：DE∥平面PAB；
（Ⅱ）求证：平面PDB⊥平面ABC；
（Ⅲ） 若PD=2，AB=
| 3 |
考点：平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：计算题,空间向量及应用
分析：（Ⅰ）利用线段成比例，直线平行；
（Ⅱ）PD⊥平面ABC，从而平面PAC⊥平面ABC；（Ⅲ）判断底面△ABC为直角三角形，或用余弦定理得AC长，求得△ABC的面积，从而由三棱锥体积公式得到答案．
（Ⅱ）PD⊥平面ABC，从而平面PAC⊥平面ABC；（Ⅲ）判断底面△ABC为直角三角形，或用余弦定理得AC长，求得△ABC的面积，从而由三棱锥体积公式得到答案．
解答：
解：（Ⅰ）∵
=
=2 ， ∴DE∥PA，…（2分）∵DE?平面PAB，PA?平面PAB，∴DE∥平面PAB；…（3分）
（Ⅱ）因为平面PAC⊥平面ABC，
且平面PAC∩平面ABC=AC，PD?平面PAC，PD⊥AC，
所以PD⊥平面ABC，…（6分）
又PD?平面PDB，
所以平面PDB⊥平面ABC．…（7分）
（Ⅲ）由（Ⅱ）可知PD⊥平面ABC．
法一：△ABC中，AB=
，∠ABC=60°，AC=3，
由正弦定理
=
，得sin∠ACB=
，
因为AC＞AB，所以∠ACB＜∠ABC，则∠ACB=
，因此∠CAB=
，…（8分）
△ABC的面积S△ABC=
AC•AB=
•3•
=
． …（10分）
所以三棱锥P-ABC的体积VP-ABC=
×S△ABC×PD=
． …（12分）
法二：△ABC中，AB=
，∠ABC=60°AC=3，由余弦定理得：AC2=AB2+BC2-2AB•BC•cos60°，
所以BC2-
BC-6=0，
所以BC=2
或-
（舍去）． …（8分）
△ABC的面积S△ABC=
AB•BC•sin60°=
•
•2
•
=
． …（10分）
所以三棱锥P-ABC的体积VP-ABC=
×S△ABC×PD=
． …（12分）
| PE |
| EC |
| AD |
| DC |
（Ⅱ）因为平面PAC⊥平面ABC，
且平面PAC∩平面ABC=AC，PD?平面PAC，PD⊥AC，
所以PD⊥平面ABC，…（6分）
又PD?平面PDB，
所以平面PDB⊥平面ABC．…（7分）
（Ⅲ）由（Ⅱ）可知PD⊥平面ABC．
法一：△ABC中，AB=
| 3 |
由正弦定理
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
| 1 |
| 2 |
因为AC＞AB，所以∠ACB＜∠ABC，则∠ACB=
| π |
| 6 |
| π |
| 2 |
△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
所以三棱锥P-ABC的体积VP-ABC=
| 1 |
| 3 |
| 3 |
法二：△ABC中，AB=
| 3 |
所以BC2-
| 3 |
所以BC=2
| 3 |
| 3 |
△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
所以三棱锥P-ABC的体积VP-ABC=
| 1 |
| 3 |
| 3 |
点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，考查三棱锥体积的求法．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
口算题天天练系列答案
相关题目
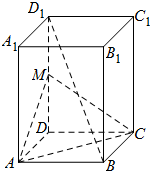已知正四棱柱ABCD-A1B1C1D1中，M是DD1的中点．
如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为菱形，点F为侧棱PC上一点．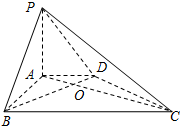
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB⊥AD，AC与BD交于点O，PA=3，AD=2，AB=2
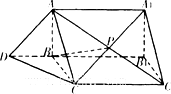直三棱柱ABC-A1B1C1中，AB⊥BC，BC=