题目内容
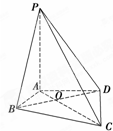 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥D-ABP和三棱锥B-PCD的体积之比.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)先证PA⊥面ABCD,得到平面PBD⊥平面PAC.(2)在求两三棱锥体积时,进行相应转化,VD-ABP=VP-ABD,VB-PCD=VP-BCD.
解答:
 解:(1)∵∠ABC=∠ADC=90°,AD=AB,AC为公共边,∴Rt△ABC≌Rt△ADC,则BO=DO,又在△ABD中,AB=AD,∴△ABD为等腰三角形,∴AC⊥BD,∵PA⊥面ABCD,∴PA⊥BD,又BD?面PBD,平面PBD⊥平面PAC.
解:(1)∵∠ABC=∠ADC=90°,AD=AB,AC为公共边,∴Rt△ABC≌Rt△ADC,则BO=DO,又在△ABD中,AB=AD,∴△ABD为等腰三角形,∴AC⊥BD,∵PA⊥面ABCD,∴PA⊥BD,又BD?面PBD,平面PBD⊥平面PAC.
(2)在Rt△ABC中,AB=1,∠BAC=60°,BC=
,∵S△ABC=
AB•ADsin120°=
×1×1×
=
,S△BCD=
BC•CDsin60°=
×
×
×
=
,∴
=
=
=
=
,
 解:(1)∵∠ABC=∠ADC=90°,AD=AB,AC为公共边,∴Rt△ABC≌Rt△ADC,则BO=DO,又在△ABD中,AB=AD,∴△ABD为等腰三角形,∴AC⊥BD,∵PA⊥面ABCD,∴PA⊥BD,又BD?面PBD,平面PBD⊥平面PAC.
解:(1)∵∠ABC=∠ADC=90°,AD=AB,AC为公共边,∴Rt△ABC≌Rt△ADC,则BO=DO,又在△ABD中,AB=AD,∴△ABD为等腰三角形,∴AC⊥BD,∵PA⊥面ABCD,∴PA⊥BD,又BD?面PBD,平面PBD⊥平面PAC.(2)在Rt△ABC中,AB=1,∠BAC=60°,BC=
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
| VD-ABP |
| VB-PCD |
| VP-ABD |
| VP-BCD |
| ||
|
| S△ABD |
| S△BCD |
| 1 |
| 3 |
点评:本题重点考查了空间面面垂直的判定及三棱锥体积公式,要根据体积将问题转化是关键,属于中档题.

练习册系列答案
相关题目
复数z满足(z-i)(2-i)=5,则复数z在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
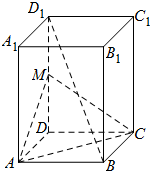 已知正四棱柱ABCD-A1B1C1D1中,M是DD1的中点.
已知正四棱柱ABCD-A1B1C1D1中,M是DD1的中点. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为菱形,点F为侧棱PC上一点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为菱形,点F为侧棱PC上一点.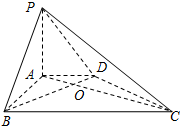 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB⊥AD,AC与BD交于点O,PA=3,AD=2,AB=2
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB⊥AD,AC与BD交于点O,PA=3,AD=2,AB=2 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,又PA⊥底面ABCD,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,又PA⊥底面ABCD,E为BC的中点.