题目内容
已知函数f（x）=x2-2x-8，g（x）=（x+1）（x-a），（a为常数）．
（1）求不等式g（x）＜0的解集；
（2）若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，求实数m的取值范围．
（1）求不等式g（x）＜0的解集；
（2）若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，求实数m的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用
分析：（1）根据二次函数以及一元二次不等式的性质即可求不等式g（x）＜0的解集；
（2）若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，利用基本不等式的性质即可求实数m的取值范围．
（2）若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，利用基本不等式的性质即可求实数m的取值范围．
解答：
解：（1）∵g（x）=（x+1）（x-a），
∴g（x）＜0，即（x+1）（x-a）＜0，
对应方程（x+1）（x-a）=0的根为x=a或x=-1，
若a=-1，则不等式无解，
若a＞-1，则（x+1）（x-a）＜0的解为-1＜x＜a，
若a＜-1，则（x+1）（x-a）＜0的解为a＜x＜-1，
综上：当a=-1，则不等式的解集为空集，
当a＞-1，则不等式的解集为（-1，a），
若a＜-1，则不等式的解集为（a，-1）；
（2）若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，
即x2-4x+7≥（m-1）x，
即m-1≤
=x+
-4，
设h（x）=x+
-7，则h（x）在（2，
）上单调递减，在（
，+∞）上单调递增，
则h（x）的最小值为h（
）=
+
-4=2
-4，
则m-1≤2
-4，
即m≤2
-3，
则实数m的取值范围是m≤2
-3．
∴g（x）＜0，即（x+1）（x-a）＜0，
对应方程（x+1）（x-a）=0的根为x=a或x=-1，
若a=-1，则不等式无解，
若a＞-1，则（x+1）（x-a）＜0的解为-1＜x＜a，
若a＜-1，则（x+1）（x-a）＜0的解为a＜x＜-1，
综上：当a=-1，则不等式的解集为空集，
当a＞-1，则不等式的解集为（-1，a），
若a＜-1，则不等式的解集为（a，-1）；
（2）若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，
即x2-4x+7≥（m-1）x，
即m-1≤
| x2-4x+7 |
| x |
| 7 |
| x |
设h（x）=x+
| 7 |
| x |
| 7 |
| 7 |
则h（x）的最小值为h（
| 7 |
| 7 |
| 7 | ||
|
| 7 |
则m-1≤2
| 7 |
即m≤2
| 7 |
则实数m的取值范围是m≤2
| 7 |
点评：本题主要考查不等式的解法以及不等式恒成立问题，利用基本不等式是解决本题的关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
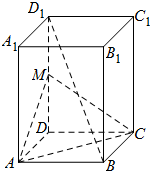已知正四棱柱ABCD-A1B1C1D1中，M是DD1的中点．
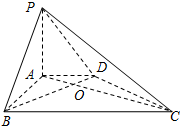如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB⊥AD，AC与BD交于点O，PA=3，AD=2，AB=2
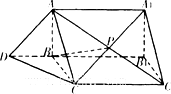直三棱柱ABC-A1B1C1中，AB⊥BC，BC=
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠ABC=60°，又PA⊥底面ABCD，E为BC的中点．