题目内容
已知θ为第二象限角,25sin2θ+sinθ-24=0,则cosθ的值为( )
A、-
| ||
B、±
| ||
C、
| ||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式变形,求出sinθ的值,根据θ为第二象限角,利用同角三角函数间基本关系求出cosθ的值即可.
解答:
解:由25sin2θ+sinθ-24=0,得到(25sinθ-24)(sinθ+1)=0,
解得:sinθ=
或sinθ=-1,
∵θ为第二象限角,
∴sinθ=
,
则cosθ=-
=-
.
故选:A.
解得:sinθ=
| 24 |
| 25 |
∵θ为第二象限角,
∴sinθ=
| 24 |
| 25 |
则cosθ=-
| 1-sin2θ |
| 7 |
| 25 |
故选:A.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
已知O是△ABC的重心,且35a
+21b
+15c
=
,则C=( )
| OA |
| OB |
| OC |
| 0 |
| A、30° | B、60° |
| C、90° | D、120° |
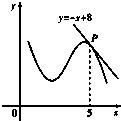 如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )A、
| ||
| B、1 | ||
| C、2 | ||
| D、0 |
函数y=2cos2(x-
)-1是( )
| π |
| 4 |
| A、最小正周期为π的奇函数 |
| B、最小正周期为2π的奇函数 |
| C、最小正周期为π的偶函数 |
| D、最小正周期为2π的偶函数 |
将4本不同的书分给3个同学,则所有的不同分法种数有( )
| A、36 | B、81 | C、64 | D、72 |
已知两条不同的直线l,m和两个不同的平面α,β,则下列命题中:①若l∥m,m?α,则l∥α,②若l∥α,m?α,则l∥m,③若l∥α,l∥β,则α∥β,④若α∥β,l∥α,则l∥β,正确命题个数是( )
| A、0 | B、1 | C、2 | D、3 |
若非零实数a,b满足a<b,则下列不等式正确的是( )
| A、a2<b2 | ||||
| B、a3<b3 | ||||
| C、|a|<b | ||||
D、
|
已知△ABC中,a=4,b=4
,∠A=30°则∠B等于( )
| 3 |
| A、300 |
| B、600 |
| C、300或1500 |
| D、600或 1200 |