题目内容

若非零实数a，b满足a＜b，则下列不等式正确的是（　　）
A、a2＜b2
B、a3＜b3
C、|a|＜b
D、
1
a
＜
1
b
考点：不等式的基本性质
专题：函数的性质及应用
分析：考察函数f（x）=x3在R上单调递增，即可得出．
解答： 解：考察函数f（x）=x3在R上单调递增，
∵a＜b，∴a3＜b3．
故选：B．
点评：本题考查了函数的单调性，属于基础题．
练习册系列答案
相关题目
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点的直线交双曲线所得弦长为2a．若这样的直线有且只有两条，则双曲线的离心率是
 
．
已知θ为第二象限角，25sin2θ+sinθ-24=0，则cosθ的值为（　　）
A、-
7
25
B、±
7
25
C、
24
25
D、
7
25
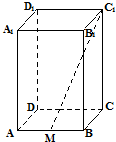如图，正四棱柱（底面是正方形的直棱柱）ABCD-A1B1C1D1的底面边长为1，高为2，M为线段AB的中点，设异面直线CD与MC1所成角为θ，则tanθ=（　　）
A、2
2
B、2
3
C、2
5
D、2
7
已知x，y满足
y≤2x
y≥-2x
x≤3
，则目标函数z=x-2y的最小值为（　　）
A、15B、-15C、9D、-9
若将函数f（x）=x5表示为f（x）=a0+a1（1+x）+a2（1+x）2+…+a5（1+x）5，其中a0，a1，a2，…，a5为实数，则a3+a5=（　　）
A、9B、10C、11D、12
1
1×2
+
1
2×3
+
1
3×4
+…+
1
9×10
等于（　　）
A、
8
9
B、
1
10
C、
9
10
D、1
若椭圆的短轴长为4
5
，它的一个焦点是（2
15
，0），则该椭圆的标准方程是（　　）
A、
x2
80
+
y2
20
B、
x2
20
+
y2
80
C、
x2
35
+
y2
20
D、
x2
20
+
y2
35
已知函数f（x）=x-
2
x
+a（2-lnx）（a∈R），讨论函数f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网