题目内容
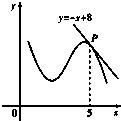如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（ ）A、
| ||
| B、1 | ||
| C、2 | ||
| D、0 |
考点：导数的运算
专题：导数的概念及应用
分析：利用函数在切点处的导数值是切线的斜率求出f′（5），将切点坐标代入切线方程求出f（5）．
解答：
解：f′（5）=-1
将x=5代入切线方程得f（5）=-5+8=3，
所以f（5）+f′（5）=3+（-1）=2，
故选：C
将x=5代入切线方程得f（5）=-5+8=3，
所以f（5）+f′（5）=3+（-1）=2，
故选：C
点评：本题考查导数的几何意义：函数在切点处的导数值是切线的斜率．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
“自然数中a，b，c恰有一个偶数”的否定为（ ）
| A、自然数a，b，c 都是奇数 |
| B、自然数a，b，c都是偶数 |
| C、自然数a，b，c中至少有两个偶数 |
| D、自然数a，b，c都是奇数或至少有两个偶数 |
已知（3x-1）8=a8x8+a7x7+a6x6+…+a1x1+a0，则 a6+a4+a2+a0的值是（ ）
| A、27+215-38 |
| B、27+215 |
| C、28-38 |
| D、28+216-1 |
对于任意的实数a，b，c，d有如下说法，其中正确的个数为 （ ）
（1）若a＞b，c＞d，则a+c＞b+d．
（2）若ac2＞bc2，则a＞b．
（3）若a＞b，则ac2＞bc2．
（4）若a＞b，c＞d，则ac＞bd．
（1）若a＞b，c＞d，则a+c＞b+d．
（2）若ac2＞bc2，则a＞b．
（3）若a＞b，则ac2＞bc2．
（4）若a＞b，c＞d，则ac＞bd．
| A、4 | B、3 | C、2 | D、1 |
已知θ为第二象限角，25sin2θ+sinθ-24=0，则cosθ的值为（ ）
A、-
| ||
B、±
| ||
C、
| ||
D、
|
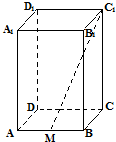如图，正四棱柱（底面是正方形的直棱柱）ABCD-A1B1C1D1的底面边长为1，高为2，M为线段AB的中点，设异面直线CD与MC1所成角为θ，则tanθ=（ ）若椭圆的短轴长为4
，它的一个焦点是（2
，0），则该椭圆的标准方程是（ ）
| 5 |
| 15 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|