题目内容
将4本不同的书分给3个同学，则所有的不同分法种数有（ ）
| A、36 | B、81 | C、64 | D、72 |
考点：计数原理的应用
专题：排列组合
分析：4本不同的书分给3个同学，每分一本书为一步，每一步有三种分法，共有4步完成这件事情，根据分步计数原理得到答案．
解答：
解：4本不同的书分给3个同学，每分一本书为一步，每一步有三种分法，共有4步完成这件事情，根据分步计数原理，所有的不同分法种数有34=81．
故选：B
故选：B
点评：本题主要考查了分步计数原理，关键是分清需要几步完成这件事情，属于基础题．
练习册系列答案
相关题目
“自然数中a，b，c恰有一个偶数”的否定为（ ）
| A、自然数a，b，c 都是奇数 |
| B、自然数a，b，c都是偶数 |
| C、自然数a，b，c中至少有两个偶数 |
| D、自然数a，b，c都是奇数或至少有两个偶数 |
对于任意的实数a，b，c，d有如下说法，其中正确的个数为 （ ）
（1）若a＞b，c＞d，则a+c＞b+d．
（2）若ac2＞bc2，则a＞b．
（3）若a＞b，则ac2＞bc2．
（4）若a＞b，c＞d，则ac＞bd．
（1）若a＞b，c＞d，则a+c＞b+d．
（2）若ac2＞bc2，则a＞b．
（3）若a＞b，则ac2＞bc2．
（4）若a＞b，c＞d，则ac＞bd．
| A、4 | B、3 | C、2 | D、1 |
已知θ为第二象限角，25sin2θ+sinθ-24=0，则cosθ的值为（ ）
A、-
| ||
B、±
| ||
C、
| ||
D、
|
已知函数f（x）是定义在R上的可导函数，且f（-1）=2，f′（x）＞2，则不等式f（x）＞2x+4的解集为（ ）
| A、（-∞，-1） |
| B、（-1，+∞） |
| C、（-1，0） |
| D、（0，+∞） |
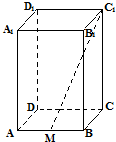如图，正四棱柱（底面是正方形的直棱柱）ABCD-A1B1C1D1的底面边长为1，高为2，M为线段AB的中点，设异面直线CD与MC1所成角为θ，则tanθ=（ ）