题目内容
对于函数f(x),若在定义域内存在实数x,满足f(-x)=-f(x),称f(x)为“局部奇函数”,若f(x)=4x-m2x+1+m2-3为定义域R上的“局部奇函数”,则实数的取值范围是( )
A、1-
| ||||
B、1-
| ||||
C、-2
| ||||
D、-2
|
考点:函数奇偶性的性质
专题:新定义
分析:根据“局部奇函数”,可知函数f(-x)=-f(x)有解即可,结合指数函数的性质,利用换元法进行求解.
解答:
解:根据“局部奇函数”的定义可知,函数f(-x)=-f(x)有解即可,
即f(-x)=4-x-m2-x+1+m2-3=-(4x-m2x+1+m2-3),
∴4x+4-x-2m(2x+2-x)+2m2-6=0,
即(2x+2-x)2-2m?(2x+2-x)+2m2-8=0有解即可.
设t=2x+2-x,则t=2x+2-x≥2,
∴方程等价为t2-2m?t+2m2-8=0在t≥2时有解,
设g(t)=t2-2m?t+2m2-8,
对称轴x=-
=m,
①若m≥2,则△=4m2-4(2m2-8)≥0,
即m2≤8,
∴-2
≤m≤2
,此时2≤m≤2
,
②若m<2,要使t2-2m?t+2m2-8=0在t≥2时有解,
则
,
即
,
解得1-
≤m<2,
综上:1-
≤m≤2
.
故选:B.
即f(-x)=4-x-m2-x+1+m2-3=-(4x-m2x+1+m2-3),
∴4x+4-x-2m(2x+2-x)+2m2-6=0,
即(2x+2-x)2-2m?(2x+2-x)+2m2-8=0有解即可.
设t=2x+2-x,则t=2x+2-x≥2,
∴方程等价为t2-2m?t+2m2-8=0在t≥2时有解,
设g(t)=t2-2m?t+2m2-8,
对称轴x=-
| -2m |
| 2 |
①若m≥2,则△=4m2-4(2m2-8)≥0,
即m2≤8,
∴-2
| 2 |
| 2 |
| 2 |
②若m<2,要使t2-2m?t+2m2-8=0在t≥2时有解,
则
|
即
|
解得1-
| 3 |
综上:1-
| 3 |
| 2 |
故选:B.
点评:本题主要考查函数的新定义,利用函数的新定义得到方程有解的条件,利用换元法将方程转化为一元二次方程有解的问题去解决是解决本题的关键.综合考查了二次函数的图象和性质.

练习册系列答案
相关题目
一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是( )
A、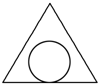 |
B、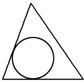 |
C、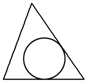 |
D、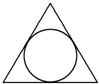 |
用“辗转相除法”求得3459和3357的最大公约数是( )
| A、3 | B、9 | C、17 | D、51 |
曲线|x|+2|y|≤4围成的区域面积是( )
| A、8 | B、16 | C、24 | D、32 |
 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).