Question

不等式组

2x+y-2≥0 x-2y+4≥0 3x-y-3≤0

表示的平面区域记为C．
（1）画出平面区域C，并求出C包含的整点个数；
（2）求平面区域C的面积．

Answer 1

考点：二元一次不等式（组）与平面区域

专题：不等式的解法及应用

分析：根据二元一次不等式组表示平面区域，作出对应的平面图形，求出整点个数，利用图形特点求区域面积即可．

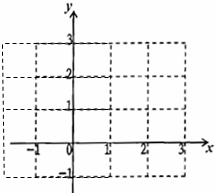
解答： 解：（1）不等式组对应的平面区域如图：
由图象可知平面区域C包含的整点个数为（0，2），（1，0），（1，1），（1，2），（2，3），共5个．
（2）平面区域C的面积梯形OABD的面积减去△OAC和△BCD的面积，
即S=

2+3

2

×2-

1

2

×1×2-

1

2

×1×3=5-1-

3

2

=4-

3

2

=

5

2

．

点评：本题主要考查二元一次不等式组表示平面区域，以及平面区域的面积求法，比较基础．