题目内容
一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是( )
A、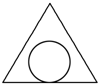 |
B、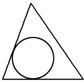 |
C、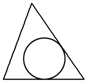 |
D、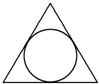 |
考点:球内接多面体,棱锥的结构特征
专题:计算题,空间位置关系与距离
分析:根据题意,设三棱锥S-ABC的各棱长均相等,作出经过侧棱SC与AB中点D的截面,得到截面△SCD,平面SCD截内切圆于圆O,由正四面体的性质与图形的对称性质加以分析,可知圆0与SD、CD相切而与SC相离.由此对照各个选项,即可得到本题答案.
解答:
 解:如图所示,设三棱锥S-ABC的各棱长均相等,球O是它的内切球,
解:如图所示,设三棱锥S-ABC的各棱长均相等,球O是它的内切球,
设H为底面△ABC的中心,根据对称性可得内切球的球心0在三棱锥的高SH上,
由SC、SH确定的平面交AB于D,连结SD、CD,得到截面△SCD,
截面SCD就是经过侧棱SC与AB中点的截面.
平面SCD与内切球相交,截得球大圆如图所示.
∵△SCD中,圆O分别与SD、CD相切于点E、H,且SD=CD,圆O与SC相离,
∴对照各个选项,可得只有B项的截面图形符合题意.
故选:B
 解:如图所示,设三棱锥S-ABC的各棱长均相等,球O是它的内切球,
解:如图所示,设三棱锥S-ABC的各棱长均相等,球O是它的内切球,设H为底面△ABC的中心,根据对称性可得内切球的球心0在三棱锥的高SH上,
由SC、SH确定的平面交AB于D,连结SD、CD,得到截面△SCD,
截面SCD就是经过侧棱SC与AB中点的截面.
平面SCD与内切球相交,截得球大圆如图所示.
∵△SCD中,圆O分别与SD、CD相切于点E、H,且SD=CD,圆O与SC相离,
∴对照各个选项,可得只有B项的截面图形符合题意.
故选:B
点评:本题给出正四面体的内切球,经过一条侧棱与对棱中点的截面与内切球相交,求所得的截面的形状.着重考查了正四面体的性质、球的性质、球与多面体的内接外切等知识,属于中档题.

练习册系列答案
相关题目
数4557、1953的最大公约数应该是( )
| A、651 | B、217 |
| C、93 | D、31 |
已知直线x+y+m=0与圆x2+y2=4交于不同的两点A,B,O是坐标原点,
+
|≥|
|,则实数m的取值范围是( )
| |OA |
| OB |
| AB |
| A、[-2,2] | ||||
B、[2,2
| ||||
C、(-2
| ||||
D、[2,2
|
对于函数f(x),若在定义域内存在实数x,满足f(-x)=-f(x),称f(x)为“局部奇函数”,若f(x)=4x-m2x+1+m2-3为定义域R上的“局部奇函数”,则实数的取值范围是( )
A、1-
| ||||
B、1-
| ||||
C、-2
| ||||
D、-2
|
 已知函数f(x)=
已知函数f(x)=