题目内容
 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),如图是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).| 分组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | ② |
| 四组 | 15≤t<20 | ① | 0.50 |
| 五组 | 20≤t≤25 | 30 | 0.30 |
| 合计 | 100 | 1.00 |
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)求旅客购票用时的平均数?
考点:频率分布直方图
专题:概率与统计
分析:(1)本题需先根据已知条件和样本容量的概念即可求出答案;
(2)本题需先根据表中所给的数据和频数与频率之间的关系即可把表补充完整;
(3)计算各个小矩形的横坐标的中间数乘以小矩形的面积之和,即为平均数.
(2)本题需先根据表中所给的数据和频数与频率之间的关系即可把表补充完整;
(3)计算各个小矩形的横坐标的中间数乘以小矩形的面积之和,即为平均数.
解答:
解:(1)样本容量是100.
(2)根据频率之和为1,求得②缺失数据为0.10,
∵样本容量为100,∴②缺失数据为50,其频率分布直方图如图:
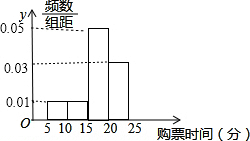
(3)旅客购票用时的平均数为7.5×0.1+12.5×0.1+17.5×0.5+22.5×0.3=17.5(min)
(2)根据频率之和为1,求得②缺失数据为0.10,
∵样本容量为100,∴②缺失数据为50,其频率分布直方图如图:

| 分组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t≤25 | 30 | 0.30 |
| 合计 | 100 | 1.00 |
点评:本题考查了频率分布直方图与频率分布表,及利用频率分布直方图求平均数,考查了学生的数据处理能力,解题的关键是读懂频率分别直方图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于函数f(x),若在定义域内存在实数x,满足f(-x)=-f(x),称f(x)为“局部奇函数”,若f(x)=4x-m2x+1+m2-3为定义域R上的“局部奇函数”,则实数的取值范围是( )
A、1-
| ||||
B、1-
| ||||
C、-2
| ||||
D、-2
|
 如图,U是全集,M、P是U的子集,则阴影部分所表示的集合是( )
如图,U是全集,M、P是U的子集,则阴影部分所表示的集合是( )| A、M∩(∁UP) |
| B、M∩P |
| C、(∁UM)∩P |
| D、(∁UM)∩(∁UP) |
曲线
+
=1与曲线
+
=1(k<3)的( )
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4-k |
| y2 |
| 3-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |