题目内容
与直线x+y+3=0相切,且圆心是(-1,0)的圆的方程为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:直线与圆的位置关系通常利用圆心到直线的距离或数形结合的方法求解,欲求圆的方程则先求出圆心和半径,根据圆与直线相切建立等量关系,解之即可.
解答:
解:圆心是(-1,0)且直线x+y+3=0与圆相切,
所以圆心到直线的距离等于半径,
即r=
=
,
所以圆C的方程为(x+1)2+y2=2;
故答案为(x+1)2+y2=2
所以圆心到直线的距离等于半径,
即r=
| |-1+3| | ||
|
| 2 |
所以圆C的方程为(x+1)2+y2=2;
故答案为(x+1)2+y2=2
点评:本题主要考查直线与圆的位置关系,以及圆的标准方程等基础知识,属于容易题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知m是平面α的一条斜线,点A∉α,为l过点A的一条动直线,那么下列情形可能出现的是( )
| A、l⊥m且l∥m |
| B、l∥m且l⊥α |
| C、l⊥m且l⊥α |
| D、l∥m且l∥α |
函数f(x)=x3+ax2+x在(0,+∞)有两个极值点,则实数a的取值范围是( )
A、(-∞,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-∞,-
|
下列向量是单位向量的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f(x)=2x+sinx+
(x∈R),f(x1)+f(x2)>0,则下列不等式正确的是( )
| 3x-1 |
| 3x+1 |
| A、x1>x2 |
| B、x1<x2 |
| C、x1+x2<0 |
| D、x1+x2>0 |
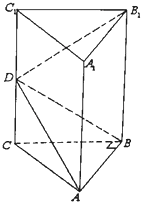 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点 函数f(x)=Asin(2x+φ),(A>0,|φ|<
函数f(x)=Asin(2x+φ),(A>0,|φ|<