题目内容
设二次函数f(x)=ax2-4bx+c(b>0)若对任意的x∈R恒有f(x)≥0成立,则
的最小值等于 .
| f(2) |
| f(-1)-f(1) |
考点:二次函数的性质
专题:函数的性质及应用,不等式
分析:首先利用二次函数f(x)≥0恒成立,解得:4b2≤ac,进一步确定c>0,通过对结果的恒等变换转化成
+
-1,最后利用均值不等式求的结果.
| a |
| 2b |
| c |
| 8b |
解答:
解:二次函数f(x)=ax2-4bx+c(b>0)若对任意的x∈R恒有f(x)≥0成立.
则:△=16b2-4ac≤0
即:4b2≤ac
所以:c>0
则:f(-1)=a+4b+c
f(1)=a-4b+c
f(-1)-f(1)=8b
=
=
+
-1
利用均值不等式
+
≥2
≥1
所以:
+
-1≥0
即
的最小值为:0
则:△=16b2-4ac≤0
即:4b2≤ac
所以:c>0
则:f(-1)=a+4b+c
f(1)=a-4b+c
f(-1)-f(1)=8b
| f(2) |
| f(-1)-f(1) |
| 4a-8b+c |
| 8b |
| a |
| 2b |
| c |
| 8b |
利用均值不等式
| a |
| 2b |
| c |
| 8b |
|
所以:
| a |
| 2b |
| c |
| 8b |
即
| f(2) |
| f(-1)-f(1) |
点评:本题考查的知识要点:二次函数f(x)≥0的条件,均值不等式的应用及相关的运算问题.

练习册系列答案
相关题目
过双曲线
-
=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若线段PF的中点为M,O为坐标原点,M在线段TP上,则|OM|-|MT|的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、b-a | B、a-b |
| C、b | D、不确定 |
设0<a<1,α,β是方程ax|loga(-x)|=1的两根,则αβ与1的大小关系是( )
| A、αβ>1 |
| B、αβ=1 |
| C、αβ<1 |
| D、不确定,与α有关 |
 已知函数y=Acos(
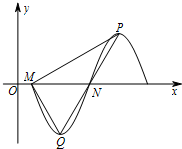
已知函数y=Acos( 已知函数f(x)=(x-a)(x-b)(其中a>b图象如图所示,则函数g(x)=ax+b是( )
已知函数f(x)=(x-a)(x-b)(其中a>b图象如图所示,则函数g(x)=ax+b是( )


