题目内容
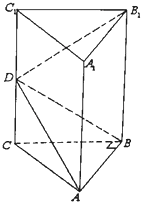 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点(1)求证:B1D⊥平面ABD;
(2)求:平面AB1D与侧面BB1C1C所成锐角的余弦的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由已知直三棱柱ABC-A1B1C1中,∠ABC=90,易得AB⊥平面BB1C1C,从而可得AB⊥DB1;由2AB=2BC=CC1=2,D是棱CC1的中点可证B1D2+BD2=BB12,即可证BD⊥B1D,从而可证;
(2)由(1)知BD⊥B1D,AD⊥B1D,则∠ADB就是平面AB1D与侧面BB1C1C的成角的平面角,Rt△ABD中求解∠ADB即可.
(2)由(1)知BD⊥B1D,AD⊥B1D,则∠ADB就是平面AB1D与侧面BB1C1C的成角的平面角,Rt△ABD中求解∠ADB即可.
解答:
(1)证明:在Rt△B1C1D中,∠B1C1D=90°,B1C1=1,C1D=
C1C=1
∴B1D=
,同理BD=
在△B1DB中,∵B1D2+BD2=B1B2,∴∠B1DB=90°
即B1D⊥BD,
又∵在直三棱柱ABC-A1B1C1中,∠ABC=90°
∴AB⊥平面BB1C1C,而B1D?平面BB1C1C,∴B1D⊥AB,
∵AB∩BD=B,∴B1D⊥平面ABD;
(2)解:由(1)知BD⊥B1D,AD⊥B1D,平面AB1D∩平面BB1C1C=B1D
∴∠ADB就是平面AB1D与侧面BB1C1C的成角的平面角
在Rt△ABD中,∠ABD=90°,AB=1,BD=
∴cos∠ADB=
.
| 1 |
| 2 |
∴B1D=
| 2 |
| 2 |
在△B1DB中,∵B1D2+BD2=B1B2,∴∠B1DB=90°
即B1D⊥BD,
又∵在直三棱柱ABC-A1B1C1中,∠ABC=90°
∴AB⊥平面BB1C1C,而B1D?平面BB1C1C,∴B1D⊥AB,
∵AB∩BD=B,∴B1D⊥平面ABD;
(2)解:由(1)知BD⊥B1D,AD⊥B1D,平面AB1D∩平面BB1C1C=B1D
∴∠ADB就是平面AB1D与侧面BB1C1C的成角的平面角
在Rt△ABD中,∠ABD=90°,AB=1,BD=
| 2 |
∴cos∠ADB=
| ||
| 3 |
点评:本小题主要考查空间中线面关系,二面角及其平面角等基础知识,考查空间想象能力、逻辑推理能力和运算求解能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
圆 C1:(x-5)2+(y-3)2=9 与圆C2:x2+y2-4x+2y-9=0 的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、内含 |
过双曲线
-
=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若线段PF的中点为M,O为坐标原点,M在线段TP上,则|OM|-|MT|的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、b-a | B、a-b |
| C、b | D、不确定 |
已知F1、F2为双曲线C:x2-y2=1的左、右焦点,点P在双曲线C上,∠F1PF2=60°,则P到y轴的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知如图是下列四个函数之一的图象,这个函数是( )


A、f(x)=ln|
| ||||
B、f(x)=ln|
| ||||
C、f(x)=
| ||||
D、f(x)=
|