Question

证明下列常见三角不等式
（1）若x∈（0，

π

2

），则sinx＜x＜tanx；
（2）若x∈（0，

π

2

），则1＜sinx+cosx≤

2

；
（3）|sinx|+|cosx|≥1．

Answer 1

考点：三角函数线

专题：三角函数的求值

分析：（1）如图所示，利用三角函数线的定义，可知sinx=MP，cosx=OM，x=

AP

，tanx=AT．从而即可证明结论．
（2）利用三角形两边之和大于第三边可得sinx+cosx＞1，结合同角三角函数的基本关系式证明（sinx+cosx）²≤2．从而证明1＜sinx+cosx≤

2

成立．
（3）分x≠

kπ

2

和x=

kπ

2

两种情况讨论，根据三角形两边之和大于第三边以及三角函数线即可得到结论．

解答： 证明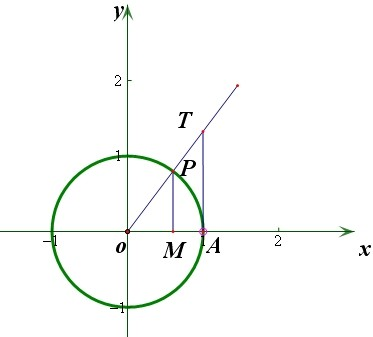：如图由三角函数线的定义可知，
sinx=MP，cosx=OM，x=

AP

，tanx=AT．
（1）∵x∈（0，

π

2

），时
S△AOP=

1

2

|OA|•|MP|=

1

2

sinx，
S扇形AOP=

1

2

AP

•|OA|=

x

2

，
S△AOT=

1

2

|OA|•|AT|=

1

2

tanx，
且S_△AOP＜S_扇形AOP＜S_AOT．
∴

1

2

sinx＜

x

2

＜

1

2

tanx
即sinx＜x＜tanx．
（2）∵x∈（0，

π

2

）时，OM＞0，MP＞0，OP＞0，
由三角形两边之和大于第三边知，
OM+MP＞OP，
∴sinx+cosx＞1．
∵（sinx+cosx）²
=1+2sinxcosx
≤1+sin²x+cos²x
=2，
∴sinx+cosx≤

2

，
∴1＜sinx+cosx≤

2

．
（3）当x≠

kπ

2

时，
由三角形两边之和大于第三边知，
|OM|+|MP|＞|OP|，
当x=

kπ

2

时，
|OM|+|MP|=|OP|，
∴|sinx|+|cosx|≥1．

点评：本题考查三角函数线的定义，同角三角函数的基本关系，三角形三边的性质等知识，利用数形结合是解决本题的关键．