题目内容
8.函数f(x)=a|log2x|+1(a≠0),定义函数F(x)=$\left\{\begin{array}{l}{f(x),x>0}\\{f(-x),x<0}\end{array}\right.$,给出下列命题:①F(x)=|f(x);
②函数F(x)是偶函数;
③当a<0时,若0<m<n<1,则有F(m)-F(n)<0成立;
④当a>0时,函数y=F(x)-2有4个零点.
其中正确命题的序号为②③④.
分析 (1)|f(x)|=|a|log2x|+1|,∴F(x)≠|f(x)|;①不对:(2)F(-x)=F(x),函数F(x)是偶函数;故②正确
(3)|log2m|>|log2n|,a|log2m|+1>a|log2n|+1,即F(m)<F(n)成立;故F(m)-F(n)<0成立;所以③正确
(4)x>0时,F(x)的最小值为F(1)=1,运用图象判断即可.
解答 解:解:(1)∵函数f(x)=a|log2x|+1(a≠0),定义函数F(x)=$\left\{\begin{array}{l}{f(x),x>0}\\{f(-x),x<0}\end{array}\right.$,
对于①,∴|f(x)|=|a|log2x|+1|,∴F(x)≠|f(x)|;故①不错;
对于②,F(x)=$\left\{\begin{array}{l}{f(x),x>0}\\{f(-x),x<0}\end{array}\right.$═F(x)∴函数F(x)是偶函数;故②正确,
对于③,∵当a<0时,若0<m<n<1,∴|log2m|>|log2n|
∴a|log2m|+1>a|log2n|+1,即F(m)<F(n)成立;故F(m)-F(n)<0成立;所以③正确;
对于④,∴x>0时,F(x)在(0,1)单调递减,(1,+∞)单调递增,∴x>0时,F(x)的最小值为F(1)=1,
故x>0时,F(x)与y=-2有2个交点,∵函数F(x)是偶函数,∴x<0时,F(x)与y=-2有2个交点
故当a>0时,函数y=F(x)-2有4个零点.所以④正确,
故答案为:②③④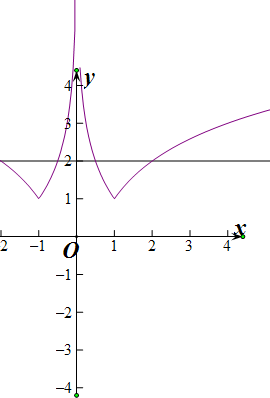
点评 本题综合考察了函数的性质,运用图象解决问题,对于函数式子与性质的结合,关键是理解,属于难题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
16.已知a=cos17°cos23°-sin17°sin23°,b=2cos225°-1,c=$\frac{{\sqrt{3}}}{2}$,则a,b,c的大小关系( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
20.在圆的方程x2+y2+Dx+Ey+F=0中,若D2=E2>4F,则圆的位置满足( )
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |