题目内容
17.已知随机变量ξ~B(n,p),若$E(ξ)=\frac{5}{3}$,$D(ξ)=\frac{10}{9}$,则n=5,p=$\frac{1}{3}$.分析 随机变量ξ~B(n,p),可得E(ξ)=np,D(ξ)=np(1-p),即可得出.
解答 解:∵随机变量ξ~B(n,p),$E(ξ)=\frac{5}{3}$,$D(ξ)=\frac{10}{9}$,
则np=$\frac{5}{3}$,np(1-p)=$\frac{10}{9}$,
解得n=5,p=$\frac{1}{3}$.
故答案为:5,$\frac{1}{3}$.
点评 本题考查了二项分布列的数学期望及其方差的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知角α的终边经过点(-4,-3),那么tanα等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
12.两个实习生每人加工一个零件,加工为一等品的概率分别为$\frac{2}{3}$和$\frac{1}{2}$,两个零件是否加工为一等品相互独立,则这两个零件中至少有一个加工为一等品的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
9.袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是( )
| A. | 至少有一个白球;至少有一个红球 | B. | 至少有一个白球;红、黑球各一个 | ||
| C. | 恰有一个白球;一个白球一个黑球 | D. | 至少有一个白球;都是白球 |
6.已知$|{\vec a}|=1$,$|{\vec b}|=2$,$\vec a(\vec a-\vec b)=3$则$\vec a$与$\vec b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | π |
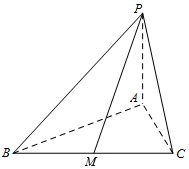 在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.
在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.