题目内容
3.已知函数f(x)=x2+$\frac{a}{x}$(x≠0,a∈R)(1)当a=0时,判断函数f(x)的奇偶性;
(2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围.
分析 (1)由已知得函数f(x)=x2(x≠0,a∈R),根据函数奇偶性的定义,可判断出f(x)=x2为偶函数;
(2)根据f(x)在区间[2,+∞)是增函数,结合函数单调性的定义,可得当x2>x1≥2,f(x1)-f(x2)<0,由此构造关于a的不等式,解不等式可得实数a的取值范围.
解答 解:(1)a=0时,f(x)=x2,显然f(-x)=f(x),定义域是(-∞,0)∪(0,+∞),关于原点对称,
故f(x)是偶函数;
(2)设x2>x1≥2,f(x1)-f(x2)=${{x}_{1}}^{2}$+$\frac{a}{{x}_{1}}$-${{x}_{2}}^{2}$-$\frac{a}{{x}_{2}}$=$\frac{{{x}_{1}-x}_{2}}{{{x}_{1}x}_{2}}$[x1x2(x1+x2)-a],
由x2>x1≥2得x1x2(x1+x2)>16,x1-x2<0,x1x2>0
要使f(x)在区间[2,+∞)是增函数只需f(x1)-f(x2)<0,
即x1x2(x1+x2)-a>0恒成立,则a≤16.
另解(导数法):f′(x)=2x-$\frac{a}{{x}^{2}}$,
要使f(x)在区间[2,+∞)是增函数,
只需当x≥2时,f'(x)≥0恒成立,即2x-$\frac{a}{{x}^{2}}$≥0,
则a≤2x3∈[16,+∞)恒成立,
故当a≤16时,f(x)在区间[2,+∞)是增函数.
点评 本题考查的知识点是函数奇偶性的性质,函数单调性的性质,熟练掌握函数奇偶性和单调性的定义,将已知转化为关于参数a的方程(不等式)是解答本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.若$α∈(0,\frac{π}{2})$,且${sin^2}α+cos2α=\frac{1}{4}$,则tanα的值等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
12.两个实习生每人加工一个零件,加工为一等品的概率分别为$\frac{2}{3}$和$\frac{1}{2}$,两个零件是否加工为一等品相互独立,则这两个零件中至少有一个加工为一等品的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
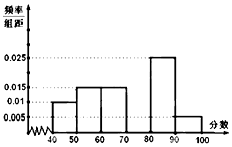 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: