题目内容

因为|
b
2a
|＞
1
2
，所以-
b
2a
的取值范围为：
 
．
考点：不等式的基本性质
专题：不等式的解法及应用
分析：由于|
b
2a
|＞
1
2
，可得-
b
2a
＞
1
2
或-
b
2a
＜-
1
2
．
解答： 解：∵|
b
2a
|＞
1
2
，
∴-
b
2a
＞
1
2
或-
b
2a
＜-
1
2
．
∴-
b
2a
的取值范围是(-∞，-
1
2
)∪(
1
2
，+∞)．
故答案为：(-∞，-
1
2
)∪(
1
2
，+∞)．
点评：本题考查了绝对值不等式的性质，属于基础题．
练习册系列答案
相关题目
在△ABC中，三边a、b、c所对的角分别为A、B、C，a=
2
，b=3，C=45°，则
AC
•
CB
=
 
．
已知二次函数f（x）=2kx2-2x-3k-2，x∈[-5，5]，求实数k的取值范围，使y=f（x）在区间[-5，5]上是单调函数．
已知集合A={x|x=a2+1，a∈N+且x≤10}，B={y|y=a2-2a+2，a∈N+且y≤10}，求A∩B，A∪B．
已知函数f（x）=sin（
π
2
+x）cos（
π
2
-x）+cosxcos（π-x）
（1）求函数f（x）的最小正周期；
（2）当x∈[-
π
4
，
π
4
]时，求函数f（x）的最大值和最小值．
已知椭圆C的中心在坐标原点，它的一个焦点坐标为（
2
，0），它的长轴是短轴的
3
倍，直线y=m（m为常数）与椭圆交于A，B两点，以线段AB为直径作圆P，圆心为P．
（1）求椭圆C的方程；
（2）若圆P与x轴相切，求圆心P的坐标；
（3）设M（x，y）是圆P上的动点，当m变化时，求y的最大值．
已知定义在R上的函数f（x），g（x）满足
f(x)
g(x)
=ax，且f′（x）g（x）＞f（x）g′（x），
f(1)
g(1)
+
f(-1)
g(-1)
=
5
2
．若有穷数列{
f(n)
g(n)
}的前n项和为Sn，则满足不等式Sn＞2015的最小正整数n等于（　　）
A、7B、8C、9D、10
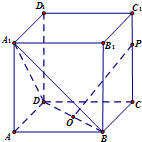（理）如图，在正方体ABCD-A1B1C1D1中，点O为线段BD的中点．设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（　　）
A、[
3
3
，1]
B、[
6
3
，1]
C、[
6
3
，
2
2
3
]
D、[
2
2
3
，1]
已知函数y=f（x）（x∈R）满足f（x+2）=f（x），且x∈（-1，1]时，f（x）=|x|，则y=f（x）与y=log7x的交点的个数为（　　）
A、4B、5C、6D、7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网