题目内容
已知定义在R上的函数f(x),g(x)满足
=ax,且f′(x)g(x)>f(x)g′(x),
+
=
.若有穷数列{
}的前n项和为Sn,则满足不等式Sn>2015的最小正整数n等于( )
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| A、7 | B、8 | C、9 | D、10 |
考点:数列与不等式的综合
专题:计算题,函数的性质及应用,等差数列与等比数列
分析:首先由已知条件结合导数大于0判断出ax为实数集上的增函数,由此得到a>1,再由
+
=
求出a的值,然后利用等比数列的前n项和公式求解n的值.
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
解答:
解:由(
)′=
,
而f′(x)g(x)>f(x)g′(x),所以(
)′>0,
即函数
=ax为实数集上的增函数,则a>1.
又
+
=
,解得a=2.
则数列{
}为数列{2n},
此数列是以2为首项,以2为公比的等比数列,
由前n项和Sn=
=2n+1-2,
由Sn>2015,得2n+1-2>2015,
由于210=1024,211=2048,
解得最小正整数n=10.
故选D.
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
而f′(x)g(x)>f(x)g′(x),所以(
| f(x) |
| g(x) |
即函数
| f(x) |
| g(x) |
又
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
则数列{
| f(n) |
| g(n) |
此数列是以2为首项,以2为公比的等比数列,
由前n项和Sn=
| 2(1-2n) |
| 1-2 |
由Sn>2015,得2n+1-2>2015,
由于210=1024,211=2048,
解得最小正整数n=10.
故选D.
点评:本题考查了函数的单调性与导数间的关系,考查了导数的运算法则,训练了利用等比数列的前n项和公式求值,是中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
下列叙述中错误的是( )
| A、A∈l,A∈α,B∈l,B∈a⇒l?α |
| B、梯形一定是平面图形 |
| C、空间中三点能确定一个平面 |
| D、A∈α,A∈β,B∈α,B∈β⇒α∩β=AB |
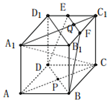 如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、
如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、