题目内容
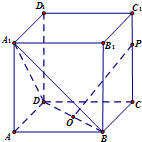 (理)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
(理)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
考点:直线与平面所成的角
专题:计算题,空间角
分析:由题意可得:直线OP于平面A1BD所成的角α的取值范围是[∠AOA1,
]∪[∠C1OA1,
],再利用正方体的性质和直角三角形的边角关系即可得出.
| π |
| 2 |
| π |
| 2 |
解答:
解:由题意可得:直线OP于平面A1BD所成的角α的取值范围是[∠AOA1,
]∪[∠C1OA1,
].
不妨取AB=2.
在Rt△AOA1中,sin∠AOA1=
=
=
.
sin∠C1OA1=sin(π-2∠AOA1)=sin2∠AOA1=2sin∠AOA1cos∠AOA1=2×
×
=
>
,
∴sinα的取值范围是[
,1].
故选:B.
| π |
| 2 |
| π |
| 2 |
不妨取AB=2.
在Rt△AOA1中,sin∠AOA1=
| AA1 |
| A1O |
| 2 | ||
|
| ||
| 3 |
sin∠C1OA1=sin(π-2∠AOA1)=sin2∠AOA1=2sin∠AOA1cos∠AOA1=2×
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
∴sinα的取值范围是[
| ||
| 3 |
故选:B.
点评:本题考查了正方体的性质和直角三角形的边角关系即可、线面角的求法,考查了推理能力,属于中档题.

练习册系列答案
相关题目
下列叙述中错误的是( )
| A、A∈l,A∈α,B∈l,B∈a⇒l?α |
| B、梯形一定是平面图形 |
| C、空间中三点能确定一个平面 |
| D、A∈α,A∈β,B∈α,B∈β⇒α∩β=AB |
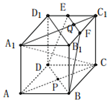 如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、
如图正方体ABCD-A1B1C1D1中,E、F分别为D1C1和B1C1的中点,P、Q分别为AC与BD、