题目内容
17.“直线y=x+b与圆x2+y2=1相交”是“0<b<1”的( )条件.| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
分析 直线y=x+b与圆x2+y2=1相交?$\frac{|b|}{\sqrt{2}}$<1,解得b.即可判断出结论.
解答 解:直线y=x+b与圆x2+y2=1相交?$\frac{|b|}{\sqrt{2}}$<1,解得$-\sqrt{2}<b<\sqrt{2}$.
∴“直线y=x+b与圆x2+y2=1相交”是“0<b<1”的必要不充分条件.
故选:C.
点评 本题考查了直线与圆的位置关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
8.4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为( )
| A. | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B. | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C. | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D. | ${C}_{4}^{2}{A}_{3}^{3}$ |
5.已知数列{an}中,a1=2,当n≥2时,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,设bn=$\frac{{a}_{n}}{{2}^{n}}$-1,则$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$等于( )
| A. | $\frac{19}{10}$ | B. | $\frac{29}{20}$ | C. | $\frac{40}{21}$ | D. | $\frac{36}{19}$ |
9.函数f(x)是定义在R上的偶函数,且 f(2)=0,当x>0时,有xf′(x)-f(x)>0恒成立,则不等式f(x)<0的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
6.下列函数中,图象的一部分符合右图的是( )
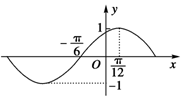

| A. | $y=sin(x+\frac{π}{6})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(2x+\frac{π}{6})$ | D. | $y=sin(2x+\frac{π}{3})$ |
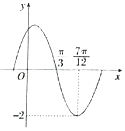 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( ) 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,$∠ABC=\frac{π}{3}$,且PA⊥平面ABCD.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,$∠ABC=\frac{π}{3}$,且PA⊥平面ABCD.