题目内容
12.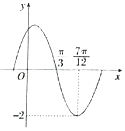 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据图象求出A,ω 和φ,即可求函数f(x)的解析式;在依次正弦函数图象及性质判断即可.
解答 解:由题设图象知,A=2.
周期T=4($\frac{7π}{12}$-$\frac{4π}{12}$)=π,
∴ω=$\frac{2π}{T}$=2.
∵点($\frac{π}{3}$,0)在函数图象上,
∴2sin(2×$\frac{π}{3}$+φ)=0,即$\frac{2π}{3}$+φ=kπ.
又∵x=$\frac{7π}{12}$时,函数f(x)取得最小值,即$\frac{7π}{6}+$φ=-$\frac{π}{2}$+2kπ.
∴同时满足条件φ=$\frac{π}{3}$.
故函数f(x)的解析式为f(x)=2sin(2x+$\frac{π}{3}$).
对于①:函数f(x)的图象向左平移$\frac{π}{6}$个单位,得到函数y=2sin(2x$+\frac{2π}{3}$),所得到的函数不是偶函数;①不对.
对于②:当x=0时,可得f(0)=2sin($\frac{π}{3}$)=$\sqrt{3}$;②不对.
对于③:最小正周期为π.③对.
对于④:f($\frac{12π}{11}$)=2sin($\frac{24π}{11}$+$\frac{π}{3}$)=2sin$\frac{83π}{33}$=2sin($2π+\frac{17π}{33}$)=2sin($\frac{17π}{33}$),
f($\frac{14π}{13}$)=2sin($\frac{28}{13}$+$\frac{π}{3}$)=2sin$\frac{97π}{39}$=2sin(2π$+\frac{11π}{13}$)=2sin($\frac{11π}{13}$),
由图象可得:sin($\frac{17π}{33}$)<0,sin($\frac{11π}{13}$)>0,∴$f(\frac{12π}{11})<f(\frac{14π}{13})$;④对.
对于⑤:f($\frac{5π}{3}-x$)=2sin($\frac{10π}{3}-2x+\frac{π}{3}$)=2sin(4π$-\frac{π}{3}$-2x)=-2sin(2x+$\frac{π}{3}$)=-f(x)
∴$f(x)=-f(\frac{5π}{3}-x)$.⑤对.
综上可得:③④⑤对.
故答案为:C.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

参考数据公式:$\sum_{i=1}^{6}$xiyi=1024.6,$\sum_{i=1}^{6}$xi2=730,$\overline{x}$=9,$\overline{y}$=$\frac{379}{30}$
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利总),那么你每月要偿还父母约多少元钱?
| A. | 5$\sqrt{13}$ | B. | 5$\sqrt{11}$ | C. | 5$\sqrt{7}$ | D. | 5 |
| A. | $-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $±\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |