题目内容
7.在△ABC中,已知:$\frac{a+b}{a}=\frac{sinB}{sinB-sinA}$,且cos(A-B)+cosC=1-cos2C.(1)判断△ABC的形状,并证明;
(2)求$\frac{a+c}{b}$的取值范围.
分析 (1)利用正弦定理和三角形内角和公式结合和与差公式可得a,b,c关系,即可判断△ABC的形状.
(2)利用正弦定理,把边转化为角,利用三角函数的有界限即可求出范围.
解答 解:(1)△ABC为直角三角形,
证明:在△ABC中,∵$\frac{a+b}{a}=\frac{sinB}{sinB-sinA}$,
根据正弦定理,得$\frac{a+b}{a}=\frac{b}{b-a}$,
∴b2-a2=ab…①
∵cos(A-B)+cosC=1-cos2C,
∴cos(A-B)-cos(A+B)=2sin2C,
化简得sinAsinB=sin2C,
由正弦定理,得ab=c2,…②
将②代入①中得b2-a2=c2,即a2+c2=b2,
故△ABC是直角三角形;
(2)由(1)知$B=\frac{π}{2}$,
则$A+C=\frac{π}{2}$,即$C=\frac{π}{2}-A$,
故$sinC=sin(\frac{π}{2}-A)=cosA$.
根据正弦定理,得$\frac{a+c}{b}=\frac{sinA+sinC}{sinB}=sinA+cosA=\sqrt{2}sin(A+\frac{π}{4})$.
∵$0<A<\frac{π}{2},\frac{π}{4}<A+\frac{π}{4}<\frac{3π}{4}$,
∴$\frac{{\sqrt{2}}}{2}<sin(A+\frac{π}{4})≤1$,
∴$1<\sqrt{2}sin(A+\frac{π}{4})≤\sqrt{2}$,
即$\frac{a+c}{b}$的取值范围是$(1,\sqrt{2}]$.
点评 本题考查了正弦定理和三角形内角和公式结合和与差公式,以及利用三角函数的有界性求范围.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点分别为F1、F2.左、右顶点分别为A、B,虚轴的上、下端点分别为C、D.若线段BC与双曲线的渐近线的交点为E,且∠BF1E=∠CF1E,则双曲线的离心率为( )
| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
19.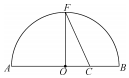 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )| A. | $\frac{a+b}{2}≥\sqrt{ab}$(a>0,b>0) | B. | a2+b2≥2ab(a>0,b>0) | ||
| C. | $\frac{2ab}{a+b}≤\sqrt{ab}$(a>0,b>0) | D. | $\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$(a>0,b>0) |
16. 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
17.“直线y=x+b与圆x2+y2=1相交”是“0<b<1”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
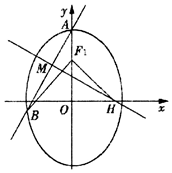 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.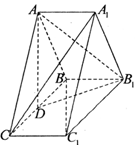 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证: