题目内容
5.已知数列{an}中,a1=2,当n≥2时,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,设bn=$\frac{{a}_{n}}{{2}^{n}}$-1,则$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$等于( )| A. | $\frac{19}{10}$ | B. | $\frac{29}{20}$ | C. | $\frac{40}{21}$ | D. | $\frac{36}{19}$ |
分析 当n≥2时,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,即有$\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}=n+1$
可得($\frac{{a}_{2}}{{2}^{2}}-\frac{{a}_{1}}{{2}_{1}})+(\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}})+…(\frac{{a}_{n}}{{2}^{2}}-\frac{{a}_{n-1}}{{2}^{n-1}})$+($\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}}$)+…+($\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}$)=1+2+…+(n-1)
bn=$\frac{{a}_{n}}{{2}^{n}}$-1=$\frac{n(n-1)}{2}$,$\frac{1}{{b}_{n}}$=2($\frac{1}{n-1}-\frac{1}{n}$)
则$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$+…+$\frac{1}{{b}_{n}}$=2($\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}-\frac{1}{n}$)即可求解
解答 解:∵当n≥2时,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,∴$\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}=n+1$
$\frac{{a}_{2}}{{2}^{2}}-\frac{{a}_{1}}{{2}^{1}}=1,\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}}=2,…\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}=n-1$
∴($\frac{{a}_{2}}{{2}^{2}}-\frac{{a}_{1}}{{2}_{1}})+(\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}})+…(\frac{{a}_{n}}{{2}^{2}}-\frac{{a}_{n-1}}{{2}^{n-1}})$+($\frac{{a}_{3}}{{2}^{3}}-\frac{{a}_{2}}{{2}^{2}}$)+…+($\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{n-1}}{{2}^{n-1}}$)=1+2+…+(n-1)
∴$\frac{{a}_{n}}{{2}^{n}}-\frac{{a}_{1}}{{2}^{1}}=\frac{(n-1)(1+n-1)}{2}=\frac{n(n-1)}{2}$
∴bn=$\frac{{a}_{n}}{{2}^{n}}$-1=$\frac{n(n-1)}{2}$,$\frac{1}{{b}_{n}}$=2($\frac{1}{n-1}-\frac{1}{n}$)
∴则$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$+…+$\frac{1}{{b}_{n}}$=2($\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}-\frac{1}{n}$)
故$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$等于2(1-$\frac{1}{20}$)=$\frac{19}{10}$
故选:A
点评 本题考查了累加法求数列通项,裂项相消法求和,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
 将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )
将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( )| A. | $\frac{32}{3}$$\sqrt{6}$cm3 | B. | $\frac{64}{3}$$\sqrt{6}$cm3 | C. | $\frac{32}{3}$$\sqrt{2}$cm3 | D. | $\frac{64}{3}$$\sqrt{2}$cm3 |
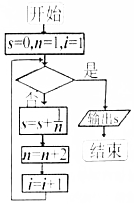
| A. | i>1010 | B. | i<1010 | C. | i>1009 | D. | i<1009 |
| A. | 5$\sqrt{13}$ | B. | 5$\sqrt{11}$ | C. | 5$\sqrt{7}$ | D. | 5 |
| A. | 恰有1名女生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名女生与全是男生 |
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |