题目内容
若实数x，y满足
，则z=2x+y的最小值为 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组表示的平面区域，由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越小，z越小，结合图象可求z的最小值．
解答：
解：作出不等式组
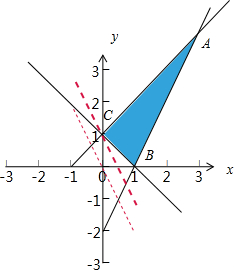
表示的平面区域，如图所示的阴影部分
由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越小，z越小
由题意可得，当y=-2x+z经过点C时，z最小
由
，可得C（0，1），
此时z=1
故答案为：1．
解：作出不等式组
|
由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越小，z越小
由题意可得，当y=-2x+z经过点C时，z最小
由
|
此时z=1
故答案为：1．
点评：本题主要考查了线性目标函数在线性约束条件下的最值的求解，解题的关键是明确z的几何意义
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知等比数列，a1=2，公比q=2，其前n项和为Sn，前n项积为Tn，那么，
等于（ ）
| lim |
| x→∞ |
| Sn | ||
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、2 |
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥CD．设f（x）为奇函数，且在（-∞，0）上递减，f（-2）=0，则xf（x）＜0的解集为（ ）
| A、（-∞，-2） |
| B、（2，+∞） |
| C、（-∞，-2）∪（2，+∞） |
| D、（-2，2） |
已知集合A={x∈R|
≤0}，B={x∈R|（x-2a）（x-a2-1）＜0}．若A∩B=∅，则实数a的取值范围是（ ）
| x-4 |
| x+1 |
| A、（2，+∞） |
| B、[2，+∞） |
| C、{1}∪[2，+∞） |
| D、（1，+∞） |