题目内容
已知集合A={x∈R|
≤0},B={x∈R|(x-2a)(x-a2-1)<0}.若A∩B=∅,则实数a的取值范围是( )
| x-4 |
| x+1 |
| A、(2,+∞) |
| B、[2,+∞) |
| C、{1}∪[2,+∞) |
| D、(1,+∞) |
考点:交集及其运算
专题:集合
分析:求出A中不等式的解集确定出A,表示出B中不等式的解集,根据A与B的交集为空集,分两种情况考虑:B为空集与B不为空集,求出满足题意a的范围即可.
解答:
解:由A中不等式变形得:(x-4)(x+1)≤0,且x+1≠0,
解得:-1<x≤4,即A=(-1,4],
由B中不等式解得:2a<x<a2+1,即B=(2a,a2+1),
∵A∩B=∅,
∴分两种情况考虑:当B=∅时,2a=a2+1,即a=1;
当B≠∅时,则有2a≥4或a2+1≤-1,即a≥2,
综上,实数a的范围为{1}∪[2,+∞).
故选:C.
解得:-1<x≤4,即A=(-1,4],
由B中不等式解得:2a<x<a2+1,即B=(2a,a2+1),
∵A∩B=∅,
∴分两种情况考虑:当B=∅时,2a=a2+1,即a=1;
当B≠∅时,则有2a≥4或a2+1≤-1,即a≥2,
综上,实数a的范围为{1}∪[2,+∞).
故选:C.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设z=3+i,则
等于( )
| 1 | ||
|
| A、3+i | ||||
| B、3-i | ||||
C、
| ||||
D、
|
若α为第三象限角,则
+
的值为( )
| cosα | ||
|
| sinα | ||
|
| A、2 | B、-2 | C、1 | D、-1 |
a=0是复数a+bi(a,b∈R)为纯虚数的( )条件.
| A、充分 | B、必要 |
| C、充要 | D、非充分非必要 |
函数f(x)=
,则f(0)=( )
| x+2 |
| A、2 | ||
| B、4 | ||
| C、0 | ||
D、
|
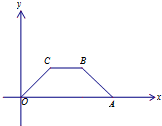 如图所示,四边形OABC是上底为1,下底为3,底角为45°的等腰梯形,由斜二测画法,画出这个梯形的直观图O′A′B′C′,在直观图中的梯形的高为( )
如图所示,四边形OABC是上底为1,下底为3,底角为45°的等腰梯形,由斜二测画法,画出这个梯形的直观图O′A′B′C′,在直观图中的梯形的高为( )