题目内容
14.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点分别为圆F1、F2,M是C上一点,|MF1|=2,且$|{\overrightarrow{M{F_1}}}||{\overrightarrow{M{F_2}}}|=-2\overrightarrow{M{F_1}}•\overrightarrow{{F_2}M}$.(1)求椭圆C的方程;
(2)当过点P(4,1)的动直线l与椭圆C相交于不同两点A,B时,线段AB上取点Q,且Q满足$|{\overrightarrow{AP}}||{\overrightarrow{QB}}|=|{\overrightarrow{AQ}}||{\overrightarrow{PB}}|$,证明点Q总在某定直线上,并求出该定直线.
分析 (1)由已知得a=2c,且$∠{F_1}M{F_2}={60^0}$,由余弦定理求出c=1.由此能求出椭圆C的方程.
(2)设直线l的方程为y=kx+(1-4k),代入椭圆方程,得(3+4k2)x2+(8k-32k2)x+64k2-32k-8=0,由此利用韦达定理、向量,结合已知条件能证明点Q总在某定直线上,并求出该定直线.
解答 解:(1)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,
左、右焦点分别为圆F1、F2,M是C上一点,|MF1|=2,且$|{\overrightarrow{M{F_1}}}||{\overrightarrow{M{F_2}}}|=-2\overrightarrow{M{F_1}}•\overrightarrow{{F_2}M}$.
∴由已知得a=2c,且$∠{F_1}M{F_2}={60^0}$,
在△F1F2M中,由余弦定理得:
(2c)2=22+(4c-2)2-2×2(4c-2)cos60°,
解得c=1.则$a=2,b=\sqrt{3}$,
所以椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
证明:(2)由题意可得直线l的斜率存在,
设直线l的方程为y-1=k(x-4),即y=kx+(1-4k),
代入椭圆方程,整理得(3+4k2)x2+(8k-32k2)x+64k2-32k-8=0,
设A(x1,y1),B(x2,y2),
则${x_1}+{x_2}=\frac{{32{k^2}-8k}}{{3+4{k^2}}},{x_1}{x_2}=\frac{{64{k^2}-32k-8}}{{3+4{k^2}}}$.
设Q(x0,y0),由$|{\overrightarrow{AP}}||{\overrightarrow{QB}}|=|{\overrightarrow{AQ}}||{\overrightarrow{PB}}|$,得:
(4-x1)(x0-x2)=(x1-x0)(4-x2)(考虑线段在x轴上的射影即可),
∴8x0=(4+x0)(x1+x2)-2x1x2,
于是$8{x_0}=({4+{x_0}})\frac{{32{k^2}-8k}}{{3+4{k^2}}}-2×\frac{{64{k^2}-32k-8}}{{3+4{k^2}}}$,
整理得3x0-2=(4-x0)k,(*)
又$k=\frac{{{y_0}-1}}{{{x_0}-4}}$,代入(*)式得3x0+y0-3=0,
∴点Q总在直线3x+y-3=0上.
点评 本题考查椭圆方程的求法,考查点总在定直线上的证明,考查直线方程的求法,考查椭圆、直线方程、向量、韦达定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| 选择套餐种类 | A | B | C |
| 选择每种套餐的人数 | 50 | 25 | 25 |
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量X表示两位顾客所得优惠金额的综合,求X的分布列和期望.
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
| 八卦 |  |  | 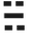 | 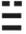 | … |  | … |
| 二进制 | 000 | 001 | 010 | 011 | … | A | … |
| 十进制 | 0 | 1 | 2 | 3 | … | B | … |
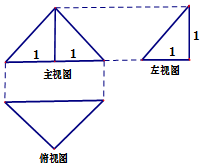
| A. | $\frac{4}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\frac{{5\sqrt{5}}}{6}π$ | D. | $\sqrt{6}π$ |
| A. | 1+$\frac{1}{2}$<2 | B. | 1+$\frac{1}{2}$+$\frac{1}{3}$<3 | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$<3 | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$<2 |
