题目内容
已知P(2,3),PA,PB是圆x2+y2-2x-2y+1=0的切线,A,B是切点,那么直线AB的方程是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:把圆的方程化为标准形式,求出圆心和半径,可得其中的一个切点A的坐标以及AB的斜率,再用点斜式求得直线AB的方程.
解答:
解:圆x2+y2-2x-2y+1=0 即圆(x-1)2+(y-1)2-2x-2y=1,表示以C(1,1)为圆心、半径等于1的圆.
故其中的一个切点A(2,1),且AB的斜率为
=
=-
,
故直线AB的方程为y-1=-
(x-2),即 x+2y-4=0,
故答案为:x+2y-4=0.
故其中的一个切点A(2,1),且AB的斜率为
| -1 |
| KCP |
| -1 | ||
|
| 1 |
| 2 |
故直线AB的方程为y-1=-
| 1 |
| 2 |
故答案为:x+2y-4=0.
点评:本题主要考查直线和圆相切的性质,用点斜式求直线的方程,属于基础题.

练习册系列答案
相关题目
若球的表面积为4π,则球的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
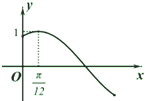 已知函数f(x)=sin(2x+φ)(0<φ<π)的部分图象,如图所示,则φ=( )
已知函数f(x)=sin(2x+φ)(0<φ<π)的部分图象,如图所示,则φ=( )A、
| ||
B、
| ||
C、
| ||
D、
|