题目内容
已知f(x)=
•
,其中
=(2cosx,-
sin2x),
=(cosx,1),x∈R.
(1)求f(x)的单调递减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=-1,a=
,且向量
=(3,sinB)与
=(2,sinC)共线,求边长b和c的值.
| a |
| b |
| a |
| 3 |
| b |
(1)求f(x)的单调递减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=-1,a=
| 7 |
| m |
| n |
考点:平面向量数量积的运算,正弦定理,余弦定理
专题:平面向量及应用
分析:(1)利用向量的数量积公式得到f(x)的解析式,然后化简求单调区间;
(2)利用向量共线,得到b,c的方程解之.
(2)利用向量共线,得到b,c的方程解之.
解答:
解:(1)由题意知f(x)=2cos2x-
sin2x=1+cos2x-
sin2x=1+2cos(2x+
).3分
∵y=cosx在a2上单调递减,∴令2kπ≤2x+
≤2kπ+π,得kπ-
≤x≤kπ+
∴f(x)的单调递减区间[kπ-
,kπ+
](k∈Z),6分
(2)∵f(A)=1+2cos(2A+
)=-1,∴cos(2A+
)=-1,又
<2A+
<
,∴2A+
=π,即A=
,8分
∵a=
,由余弦定理得a2=b2+c2-2bccosA=(b+c)2-3bc=7.10分
因为向量
=(3,sinB)与
=(2,sinC)共线,所以2sinB=3sinC,由正弦定理得2b=3c.
∴b=3,c=2.12 分.
| 3 |
| 3 |
| π |
| 3 |
∵y=cosx在a2上单调递减,∴令2kπ≤2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
∴f(x)的单调递减区间[kπ-
| π |
| 6 |
| π |
| 3 |
(2)∵f(A)=1+2cos(2A+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵a=
| 7 |
因为向量
| m |
| n |
∴b=3,c=2.12 分.
点评:本题考查了向量的数量积公式的运用以及三角函数的化简与性质的运用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
设z=x+y,其中实数x,y满足
,则z的最大值为( )
|
| A、12 | B、6 | C、0 | D、-6 |
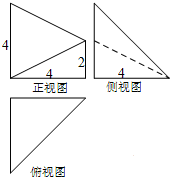 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V=
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V= 如图根据下列三视图,想象物体原形,并画出物体的实物草图.
如图根据下列三视图,想象物体原形,并画出物体的实物草图.